D. C. Pandey Solutions for Chapter: Rotation, Exercise 2: Excercise 2

As shown in the figure, a bob of mass $m$ is tied by a massless string whose other end portion is wound on a flywheel (disc) of radius $r$ and mass $m$. When released from rest the bob starts falling vertically. When it has covered a distance of $h$ the angular speed of the wheel will be

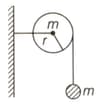
A rigid massless rod of length $3 l$ has two masses attached at each end as shown in the figure. The rod is pivoted at point $P$ on the horizontal axis (see figure). When released from initial horizontal position, its instantaneous angular acceleration will be

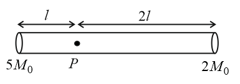
A circular disc $D_1$ of mass $M$ and radius $R$ has two identical discs $D_2$ and $D_3$ of the same mass $M$ and radius $R$ attached rigidly at its opposite ends (see figure). The moment of inertia of the system about the axis $OO\text{'}$ passing through the centre of $D_1$, as shown in the figure will be

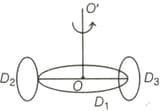
A semicircular disc of mass $M$ and radius $R$ is free to rotate about its diameter. The moment of inertia of semicircular disc about a line perpendicular to its plane through centre is

A uniform solid cylindrical roller of mass $m$ is being pulled on horizontal surface with force $F$ parallel to the surface applied at its centre. If the acceleration of the cylinder is $a$ and it is rolling without slipping, then the value of $F$ is

A solid sphere of $100 \mathrm{kg}$ and radius $10 \mathrm{m}$ moving in a space becomes a circular disc of radius $20 \mathrm{m}$ in one hour. Then the rate of change of moment of inertia in the process is

Two identical discs are moving with the same kinetic energy. One rolls and the other slides. The ratio of their speeds is

A solid sphere rolls down from the top of an inclined plane, $7 \mathrm{m}$ high, without slipping. Its linear speed at the foot of the plane is $\left(g=10 \mathrm{m} {\mathrm{s}}^{-2}\right)$