David Weber, Talei Kunkel, Alexander Martinez and, Rebecca Shultis Solutions for Chapter: Probability Games and Play, Exercise 28: Unit review

Dungeons and Dragons is a very popular role-playing game where players are given a character and embark on adventures in fantasy land. A Dungeon Master controls the game, creating scenarios and challenges for the players. Many of the actions are taken in Dungeons and Dragons rely on rolling dice that have 4, 6, 8, 10, 12 or 20 sides. Suppose you are rolling an 8-sided die.

Determine which events are impossible, unlikely, equally likely as unlikely, likely and certain. $\mathrm{P}\left(2\right)$, $\mathrm{P}\left(2,3\mathrm{or}4\right)$, $\mathrm{P}\left(\mathrm{even}\right)$, $\mathrm{P}\left(<5\right)$, $\mathrm{P}\left(9\right)$, and $\mathrm{P}\left(1,3,4,7,8\right)+\mathrm{P}\left(2,5,6\right)=1$

In the game of Risk, players set up armies on a map of the world that acts as the game board.

Players can add to their armies or wage war against armies in regions that are beside them. In these wars, each player rolls one or more six-sided dice, with each die representing a battle. With each battle, if the person initiating the war (the attacker) has a higher number, then he/she wins the battle. If the defender rolls a number that is equal to or greater than the attacker, then the defender wins the battle.

The number of dice rolled depends on the number of armies you have. When more than one die is rolled, whoever wins the most battles, wins the war. If each player wins the same number of battles, the defender wins the war.

Suppose each player rolls just one die. Find the probability that the defender wins the war if the attacker rolls a $3$. (Write the answer up to two decimal place).

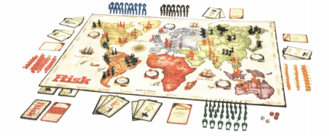
In the game of Risk, players set up armies on a map of the world that acts as the game board.

Players can add to their armies or wage war against armies in regions that are beside them. In these wars, each player rolls one or more six-sided dice, with each die representing a battle. With each battle, if the person initiating the war (the attacker) has a higher number, then he/she wins the battle. If the defender rolls a number that is equal to or greater than the attacker, then the defender wins the battle.

The number of dice rolled depends on the number of armies you have. When more than one die is rolled, whoever wins the most battles, wins the war. If each player wins the same number of battles, the defender wins the war.

Suppose each player rolls just one die. Find the probability that the defender wins the war if the attacker rolls a $1$.

In the game of Risk, players set up armies on a map of the world that acts as the game board.

Players can add to their armies or wage war against armies in regions that are beside them. In these wars, each player rolls one or more six-sided dice, with each die representing a battle. With each battle, if the person initiating the war (the attacker) has a higher number, then he/she wins the battle. If the defender rolls a number that is equal to or greater than the attacker, then the defender wins the battle.

The number of dice rolled depends on the number of armies you have. When more than one die is rolled, whoever wins the most battles, wins the war. If each player wins the same number of battles, the defender wins the war.

Suppose each player rolls just one die. Find the probability that the defender wins the war if the attacker rolls a $5$. (Write the answer up to two decimal place)

In the game of Risk, players set up armies on a map of the world that acts as the game board.

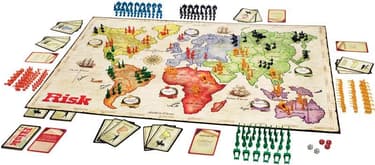
Players can add to their armies or wage war against armies in the regions that are beside them. In these wars, each player rolls one or more six-sided dice, with each die representing a battle. With each battle, if the person initiating the war (the attacker) has higher number, then he/she wins the battle. If the defender rolls a number that is equal to or greater than the attacker, then the defender wins the battle.

The number of dice rolled depends on the number of armies you have. When more than one dice is rolled, whoever wins the most battles, wins the war. If each player wins the same number of battles, the defender wins the war.

Suppose each player rolls just one die. Find the probability that the defender wins if the attacker rolls a $6$ (rounded off to two decimal places).

Suppose each player rolls two dice. Each player's highest number is compared with their opponent's, with the winner of each battle being the higher number for that battle. The lower numbers are then compared in the same way. Write the sample space for all possible outcomes of the defender's roll when the attacker has rolled a $2$ and a $5$. Create a table like the one stated below, for example. And remember, if each player wins one battle, then the defender wins the war.

In the game of Risk, players set up armies on a map of the world that acts as the game board.

Players can add to their armies or wage war against armies in regions that are beside them. In these wars, each player rolls one or more six-sided dice, with each die representing a battle. With each battle, if the person initiating the war (the attacker) has a higher number, then he/she wins the battle. If the defender rolls a number that is equal to or greater than the attacker, then the defender wins the battle. The number of dice rolled depends on the number of armies you have. When more than one die is rolled, whoever wins the most battles, wins the war. If each player wins the same number of battles, the defender wins the war. Find the probability of the defender winning the war (by winning one or both battle )

Write the answer up to three decimal place.

In the game of Risk, players set up armies on a map of the world that acts as the game board

Players can add to their armies or wage war against armies in regions that are beside them. In these wars, each player rolls one or more six-sided dice, with each die representing a battle. With each battle, if the person initiating the war (the attacker) has a higher number, then he/she wins the battle. If the defender rolls a number that is equal to or greater than the attacker, then the defender wins the battle. The number of dice rolled depends on the number of armies you have. When more than one die is rolled, whoever wins the most battles, wins the war. If each player wins the same number of battles, the defender wins the war.What attacker rolls will result in the defender's probability of winning both battles be 1