David Weber, Talei Kunkel, Rose Harrison and, Fatima Remtulla Solutions for Chapter: Triangles Principles, Processes and Solutions, Exercise 24: Practice 3
David Weber Mathematics Solutions for Exercise - David Weber, Talei Kunkel, Rose Harrison and, Fatima Remtulla Solutions for Chapter: Triangles Principles, Processes and Solutions, Exercise 24: Practice 3
Attempt the practice questions on Chapter 2: Triangles Principles, Processes and Solutions, Exercise 24: Practice 3 with hints and solutions to strengthen your understanding. MYP Mathematics A concept-based approach 3 solutions are prepared by Experienced Embibe Experts.
Questions from David Weber, Talei Kunkel, Rose Harrison and, Fatima Remtulla Solutions for Chapter: Triangles Principles, Processes and Solutions, Exercise 24: Practice 3 with Hints & Solutions
Just as in mathematics, principles in physics often lead to other useful results. Fermat's principle states that light travels in a path that requires the least time. How light behaves when reflected off a surface (called the law of reflection) can be derived from this principle. The law of reflection states that when light hits a reflective surface at an angle, it will reflect off that surface at the same angle.
According to the law of reflection, which angles will be congruent? Indicate these on a copy of the diagram.
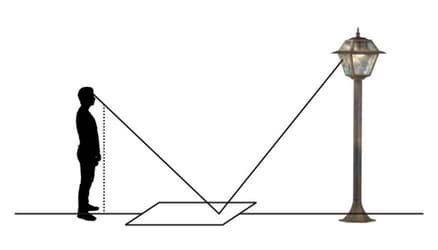
Just as in mathematics, principles in physics often lead to other useful results. Fermat's principle states that light travels in a path that requires the least time. How light behaves when reflected off a surface (called the law of reflection) can be derived from this principle. The law of reflection states that when light hits a reflective surface at an angle, it will reflect off that surface at the same angle.
Show that this produces two similar triangles and state the postulate you used.
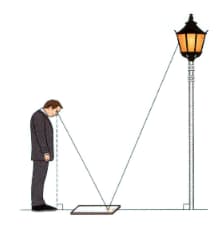
Just as in mathematics, principles in physics often lead to other useful results. Fermat's principle states that light travels in a path that requires the least time. How light behaves when reflected off a surface (called the law of reflection) can be derived from this principle. The law of reflection states that when light hits a reflective surface at an angle, it will reflect off that surface at the same angle.
Describe how this information could be used to find the height of the lamppost.
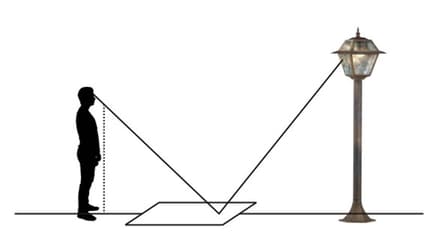
Just as in mathematics, principles in physics often lead to other useful results. Fermat's principle states that light travels in a path that requires the least time. How light behaves when reflected off a surface (called the law of reflection) can be derived from this principle. The law of reflection states that when light hits a reflective surface at an angle, it will reflect off that surface at the same angle.
What measurements would you need to know in order to actually calculate the height of the lamppost?
Thales was a Greek mathematician, philosopher and a teacher of Pythagoras. He supposedly asked the Egyptian priests how tall the Great Pyramid of Cheops was and when they refused to tell him, he set out to solve the problem himself. One method that he is said to have used involved measuring shadows. Thales, who was tall, measured his shadow to be . At exactly the same time, he measured the shadow of the pyramid to be . Draw a diagram of this situation. Indicate the similar triangles and justify how you know that the triangles are similar.
Thales was a Greek mathematician, philosopher and a teacher of Pythagoras. He supposedly asked the Egyptian priests how tall the Great Pyramid of Cheops was and when they refused to tell him, he set out to solve the problem himself. One method that he is said to have used involved measuring shadows. Thales, who was tall, measured his shadow to be . At exactly the same time, he measured the shadow of the pyramid to be . Find the height of the Great pyramid as calculated by Thales.
Thales was a Greek mathematician, philosopher and a teacher of Pythagoras. He supposedly asked the Egyptian priests how tall the Great Pyramid of Cheops was and when they refused to tell him, he set out to solve the problem himself. One method that he is said to have used involved measuring shadows. Thales, who was tall, measured his shadow to be . At exactly the same time, he measured the shadow of the pyramid to be .
Thales did not actually have to use similar triangles to find the height of the pyramid. He could have waited until his shadow was the same length as his height. explain how this would have helped him to determine the height of the pyramid.
George has a right-angled isosceles triangle and Prita has a similar triangle which has a hypotenuse of . The area of prita's triangle is four times the area of George's triangle. Find the dimensions of George's triangle.
