Dean Chalmers and Julian Gilbey Solutions for Chapter: Probability, Exercise 7: EXERCISE 4E
Dean Chalmers Mathematics Solutions for Exercise - Dean Chalmers and Julian Gilbey Solutions for Chapter: Probability, Exercise 7: EXERCISE 4E
Attempt the free practice questions on Chapter 4: Probability, Exercise 7: EXERCISE 4E with hints and solutions to strengthen your understanding. Cambridge International AS & A Level Mathematics : Probability & Statistics 1 Course Book solutions are prepared by Experienced Embibe Experts.
Questions from Dean Chalmers and Julian Gilbey Solutions for Chapter: Probability, Exercise 7: EXERCISE 4E with Hints & Solutions
The histogram shown represents the times taken, in minutes, for men to complete a task. Two men are selected at random from the group. Find the probability that the:
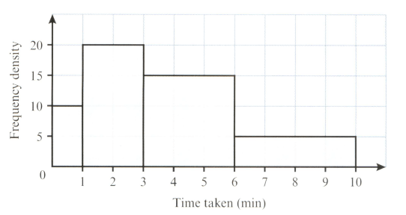
second man took less than minutes, given that the first man took less than minute.
At an insurance company, of the staff are male and work full-time . The following Venn diagram shows this and one other piece of information.
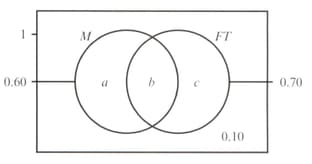
An employee is randomly selected. Find:
At an insurance company, of the staff are male and work full-time . The following Venn diagram shows this and one other piece of information.
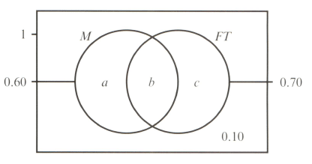
An employee is randomly selected. Find:
At an insurance company, of the staff are male and work full-time . The following Venn diagram shows this and one other piece of information.
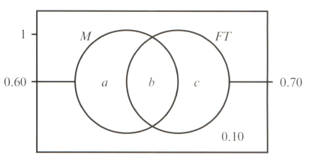
An employee is randomly selected. Find:
.
Two fair triangular spinners, both with sides marked and , are spun. Given that the sum of the two numbers spun is even, find the probability that the two numbers are the same.
Two ordinary fair dice are rolled and the two numbers rolled are added together to give the score. Given that a player's score is greater than , find the probability that it is not greater than
The circular archery target shown, on which or points can be scored, is divided into four parts of unequal area by concentric circles. The radii of the circles are and .
You may assume that a randomly fired arrow pierces just one of the four areas and is equally likely to pierce any part of the target.
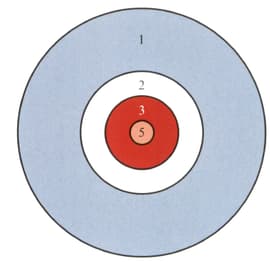
Given that an arrow does not score points, find the probability that it scores point.
The circular archery target shown, on which or points can be scored, is divided into four parts of unequal area by concentric circles. The radii of the circles are and .
You may assume that a randomly fired arrow pierces just one of the four areas and is equally likely to pierce any part of the target.
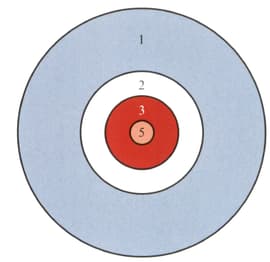
Given that a total score of points is obtained with two randomly fired arrows, find the probability that neither arrow scores point.
