Embibe Experts Solutions for Chapter: Circular Motion, Exercise 3: Exercise - 3

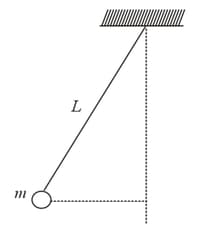
A ball of mass $\left(m\right) 0.5 \mathrm{kg}$ is attached to the end of a string having length $\left(L\right) 0.5 \mathrm{m}$. The ball is rotated on a horizontal circular path about a vertical axis. The maximum tension that the string can bear is $324 \mathrm{N}$. The maximum possible value of the angular velocity of ball (in $\mathrm{rad} {\mathrm{s}}^{-1}$) is :

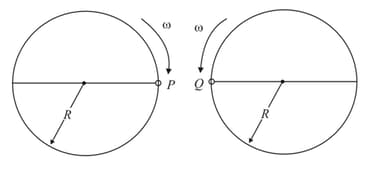
Two identical discs of the same radius $R$ are rotating about their axes in opposite directions with the same constant angular speed $\omega$. The disc is in the same horizontal plane.At time $t\mathit{ }= 0$, the points $P$ and $Q$ are facing each other as shown in the figure. The relative speed between the two points $P$ and $Q$ is $v_{\mathit{r}}$ as a function of times best represented by

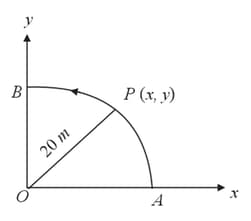
A point $P$ moves in a counter-clockwise direction on a circular path as shown in the figure. The movement of $\mathit{‘}P\mathit{’}$ is such that it sweeps out a length $s=t^3+5$, where $s$ is in meters and $t$ is in seconds. The radius of the path is $20 \mathrm{m}$. The acceleration of $‘P’$ when $t=2 \mathrm{s}$ is nearly

For a particle in uniform circular motion, the acceleration $a$ at a point $P(R,\mathrm{\theta })$ on the circle of radius $R$ is (here $\mathrm{\theta }$ is measured from the $x$-axis)

Two cars of masses $m_1$ and $m_2$ are moving in circles of radii $r_1$ and $r_2$, respectively. Their speeds are such that they make complete circles in the same time $t$. The ratio of their centripetal acceleration is:

A particle is moving with a uniform speed in a circular orbit of radius $R$ in a central force inversely proportional to the $n^{\mathrm{th}}$ power of $R$. If the period of rotation of the particle is $T$, then: