Embibe Experts Solutions for Chapter: Electromagnetic Induction, Exercise 4: Exercise - 4

A uniformly charged ring of radius$0.1 \mathrm{m}$ rotates at a frequency of ${10}^4 \mathrm{rps}$ about its axis. Find the ratio of energy density of electric field to the energy density of the magnetic field at a point on the axis at distance $0.2 \mathrm{m}$ from the centre. (Use speed of light $c=3\times {10}^8 \mathrm{m} {\mathrm{s}}^{-1}, {\mathrm{\pi }}^2 = 10$)

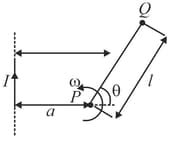
In the figure shown a long conductor carries constant current $I$. A rod $PQ$ of length $l$ is in the plane of the rod. The rod is rotated about point $P$ with constant angular velocity $\mathrm{\omega }$ as shown in the figure. Find the emf induced in the rod in the position shown. Indicate which point is at high potential.

An infinitely small bar magnet of dipole moment $M$ is moving with the speed $v$ in the $X$-direction. A small closed circular conducting loop of radius $a$ and negligible self-inductance lies is the $Y-Z \mathrm{plane}$ with its centre at$x=0$ and its axis coinciding with the $X$-axis. Find the force opposing the motion of the magnet, if the resistance of the loop is$R.$ Assume that the distance $x$ of the magnet from the centre of the loop is much greater than $a$.

A square loop of side $a=12 \mathrm{cm}$ with its sides parallel to $x,$ and $y-$axis is moved with velocity,$v=8 \mathrm{cm} {\mathrm{s}}^{-1}$ in the positive $x-$direction in a magnetic field along the positive $z-$direction. The field is neither uniform in space nor constant in time. It has a gradient $\frac{\partial B}{\partial x}={10}^{–3 } \mathrm{T} {\mathrm{cm}}^{-1}$ along the x-direction, and it is changing in time at the rate$\frac{\partial B}{\partial t}= 7 \mathrm{T} {\mathrm{cm}}^{-1}$ in the loop if its resistance is, $R=4.5 \mathrm{\Omega }.$ Find the current. 

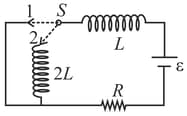
In the circuit shown, the switch S is shifted to the position $2$ from the position $1$ at, $t=0,$having been in position 1 for a long time. Find the current in the circuit as a function of time.

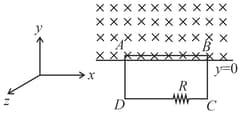
A square loop $ABCD$ of side, $l$ is moving in $xy$ plane with velocity,$\overrightarrow{\mathrm{v}}=\beta t\hat{\mathrm{j}}$. There exists a non-uniform magnetic field $\overrightarrow{B }=–B_0(1+\alpha y^2)\hat{\mathrm{k}} (y>0),$

where $B_0 \& \mathrm{\alpha }$ are positive constants. Initially, the upper wire of the loop is at $y=0$. Find the induced voltage across the resistance $R$ as a function of time. Neglect the magnetic force due to induced current.

A long solenoid of length $l= 2.0\mathrm{m},$radius $r=0.1 \mathrm{m}$ and total number of turns $N=1000$ is carrying a current$i_0=20.0 \mathrm{A}.$ The axis of the solenoid coincides with the $\mathrm{z}-\mathrm{axis}.$

$\left(\mathrm{a}\right)$ State the expression for the magnetic field of the solenoid and calculate its value? Magnetic field.

$\left(\mathrm{b}\right)$ Obtain the expression for the self-inductance $\left(L\right)$of the solenoid. Calculate its value. Value of $L$.

$\left(\mathrm{c}\right)$ Calculate the energy stored $\left(E\right)$when the solenoid carries this current?

$\left(\mathrm{d}\right)$ Let the resistance of the solenoid be $R.$ It is connected to a battery of emf e. Obtain the expression
for the current $\left(\mathrm{i}\right)$ in the solenoid.

$\left(\mathrm{e}\right)$ Let the solenoid with resistance $R$ described in part $\left(\mathrm{d}\right)$be stretched at a constant speed $\upsilon$ ($l$ is increased but $N$ and $\mathrm{\gamma }$ are constant). State Kirchhoff’s second law for this case. (Note: Do not solve for the current.)

$\left(\mathrm{f}\right)$ Consider a time varying current $i=i_0 \cos \left(\mathrm{\omega t}\right)$(where$i_0=20.0 \mathrm{A}$) flowing in the solenoid. Obtain an expression for the electric field due to the current in the solenoid. (Note: Part (e) is not operative, i.e., the solenoid is not being stretched.)

$\left(\mathrm{g}\right)$ Consider $t=\frac{\pi }{2\omega } \text{and} \omega =\frac{200}{\pi } \mathrm{rad}–{\mathrm{s}}^{–1}$ in the previous part. Plot the magnitude of the electric field as a function of the radial distance from the solenoid. Also, sketch the electric lines of force.

The wire loop shown in the figure lies in uniform magnetic induction $B=B_0\cos \omega t$ perpendicular to its plane. Given, $(r_1=10 \mathrm{cm} \& r_2=20 \mathrm{cm}, B_0=20 \mathrm{mT} \& \omega =100\mathrm{\pi })$ Find the amplitude of the current induced in the loop if its resistance is$0.1 \mathrm{\Omega } {\mathrm{m}}^{-1}$.