Embibe Experts Solutions for Chapter: Gravitation, Exercise 1: Exercise - 1

Three equal masses each of mass $m$ are placed at the three-corners of an equilateral triangle of side $a$. 

If above given three particles system of equilateral triangle side $a$ is to be changed to side of $2a$, then work done on the system is equal to:

Three equal masses each of mass $m$are placed at the three-corners of an equilateral triangle of side $a$.

In the above given three-particle system, if two particles are kept fixed and the third particle is released. Then speed of the particle when it reaches the mid-point of the side connecting the other two masses:

Periodic-time of satellite revolving around the earth is -($\mathrm{\rho }$ is density of earth)

An artificial satellite of the earth releases a package. If air resistance is neglected the point where the package will hit (with respect to the position at the time of release) will be

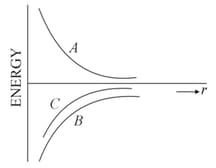
The figure shows the variation of energy with the orbit radius of a body in circular planetary motion. Find the correct statement about the curves A, B and C

A planet of mass $m$ revolves around the sun of mass $M$ in an elliptical orbit. The minimum and maximum distance of the planet from the sun are $r_{1 }\& r_2$, respectively. If the minimum velocity of the planet is $\sqrt{\frac{2GM{r}_1}{\left(r_1+r_2\right)r_2}}$ then it's maximum velocity will be

The escape velocity for a body projected vertically upwards from the surface of earth is $11 \mathrm{km} {\mathrm{s}}^{-1}$. If the body is projected at an angle of $45º$ with the vertical, the escape velocity will be 

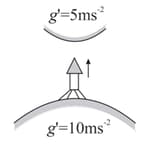
If acceleration due to gravity on the surface of earth is $10 {\mathrm{ms}}^{–2}$ and let acceleration due to gravitational acceleration at surface of another planet of our solar system be $5 {\mathrm{ms}}^{–2}$. An astronaut weighing $50 \mathrm{kg}$ on earth goes to this planet in a spaceship with a constant velocity. The weight of the astronaut with time of flight is roughly given by,