Embibe Experts Solutions for Chapter: Kinetic Theory of Gases, Exercise 1: Exercise - 1

The mean speed of the molecules of a hydrogen sample equals the mean speed of the molecules of a helium sample. Calculate the ratio of the temperature of the hydrogen sample to the temperature of the helium sample.

$0.04 \mathrm{g}$ of $\mathrm{He}$ is kept in a closed container, initially at $100.0°\mathrm{C}$. The container is now heated. Neglecting the expansion of the container, calculate the temperature at which the internal energy is increased by $12 \mathrm{J}$.

For a gas sample with $N_0$ number of molecules, the function $N\left(V\right)$ is given by, $N\left(V\right)=\frac{dN}{dV}=\left(\frac{3N_0}{V_0^3}\right)V^2$ for $0<V<V_0$ and $N\left(V\right)=0$ for $V>V_0$. Where $dN$ is a number of molecules in speed range $V$ to $V+dV$. The rms speed of the molecules is

$A, B$ and $C$ Are three closed vessels, at the same temperature $T$ And contain gases which obey the Maxwellian distribution of velocities. Vessel $A$ Contains only undefined and $C$ A mixture of equal quantities of $O_2$ And undefined. If the average speed of $O_2$ Molecules in vessel $A$ is $v_1$, that of the undefined molecules in vessel $B$ is $v_2$, the average speed of the $O_2$ Molecules in vessel $C$ is

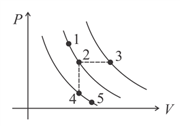
A certain gas is taken to the five states represented by dots in the graph. The plotted lines are isotherms. The order of the most probable speed $v_{\mathrm{p}}$ of the molecules at these five states is,

The pressure of an ideal gas is written as, $E=\frac{3PV}{2}$. Here, $E$ stands for,

The quantities which remain same for all ideal gases at the same temperature is/are,

One mole of an ideal gas undergoes a process in which, $T=T_0+a{V}^3$, where $T_0$ and $a$ are positive constants and $V$ is volume. The minimum pressure attainable is,