Embibe Experts Solutions for Chapter: Kinetic Theory of Gases, Exercise 3: Exercise - 3

A mixture of $2$ moles of helium gas (atomic mass$=4 \mathrm{amu}$) and $1$ mole of argon gas (atomic mass$=40 \mathrm{amu}$) is kept at $300 \mathrm{K}$ in a container. The ratio of the rms speed $\left(\frac{v_{\mathrm{rms}}\left(\mathrm{helium}\right)}{v_{\mathrm{rms}}\left(\mathrm{argon}\right)}\right)$ is

Two non-reactive monoatomic ideal gases have their atomic masses in the ratio $2:3$. The ratio of their partial pressure, when enclosed in a vessel kept at a constant temperature is $4:3$. The ratio of their densities is

One kg of a diatomic gas is at a pressure of $8\times {10}^4 \mathrm{N} {\mathrm{m}}^{-2}$ . The density of the gas is $4 \mathrm{kg} {\mathrm{m}}^{-3}$ . What is the energy of the gas due to its thermal motion?

Three perfect gases at absolute temperature $T_1, T_2$ and $T_3$ are mixed. The masses of molecules are $m_1$, $m_2$ and $m_3$ and the number of molecules are $n_1, n_2$ and $n_3$, respectively. Assuming no loss of energy, the final temperature of the mixture is

A container with insulating walls is divided into two equal parts by a partition fitted with a valve. One part is filled with an ideal gas at a pressure $p$ and temperature $T$ whereas the other part is completely evacuated. If the valve is suddenly opened, then the pressure and temperature of the gas will be

The value of $q$ is undefined. Consider an ideal gas confined in an isolated closed chamber. As the gas undergoes an adiabatic expansion, the average time of collision between molecules increases as undefined. where $v$ is the volume of the gas.

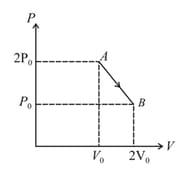
$n \mathrm{moles}$ of an ideal gas undergoes a process $A\to B$ as shown in the figure. The maximum temperature of the gas during the process will be

The temperature of an open room of volume $30 {\mathrm{m}}^3$ increased from $17º\mathrm{C} \text{to} 27º\mathrm{C}$ due to the sunshine. The atmospheric pressure in the room remains $1\times {10}^5 \mathrm{Pa}$. If $n_{i }$and $n_f$ are the number of molecules in the room before and after heating, then $n_f – n_i$ will be