Embibe Experts Solutions for Chapter: Thermodynamics, Exercise 4: Exercise - 4

A thermally insulated, the closed copper vessel contains water at $15 °\mathrm{C}$. When the vessel is shaken vigorously for $15 \min$, the temperature rises to $17 °\mathrm{C}$. The mass of the vessel is $100 \mathrm{g}$ and that of the water is $200 \mathrm{g}$. The specific heat capacities of copper and water are $420 \mathrm{J} {\mathrm{kg}}^{-1} {\mathrm{K}}^{-1}$ and $4200 \mathrm{J} {\mathrm{kg}}^{-1} {\mathrm{K}}^{-1}$, respectively. Neglect any thermal expansion.

$\left(\mathrm{a}\right)$ How much heat is transferred to the liquid-vessel system?

$\left(\mathrm{b}\right)$ How much work has been done on this system?

$\left(\mathrm{c}\right)$ How much is the increase in internal energy of the system?

One gram of water $\left(\mathrm{volume}=1 {\mathrm{cm}}^3\right)$ becomes $1671 {\mathrm{cm}}^3$ of steam when boiled at a pressure of one atmosphere. Latent heat of vaporization at this pressure is $539 \mathrm{cal} {\mathrm{gm}}^{-1}$. Compute the work done. $\left[1 \mathrm{atm}=1.013\times {10}^5 \mathrm{N} {\mathrm{m}}^{-2}\right]$

A piston can freely move inside a horizontal cylinder closed from both ends. Initially, the piston separates the inside space of the cylinder into two equal parts, each of volume $V_0$, in which an ideal gas is contained under the same pressure $p_0$ and at the same temperature. What work has to be performed in order to increase, isothermally, the volume of one part of the gas $\eta$ times compared to that of the other, by slowly moving the piston?

A cylindrical tube with adiabatic walls having volume $2V_0$contains an ideal monoatomic gas as shown in figure. The tube is divided into two equal parts by a fixed super conducting wall. Initially, the pressure and the temperature are $P_0, T_0$ on the left and $2P_0, 2T_0$ on the right. When system is left for sufficient amount of time the temperature on both sides becomes equal (a) Find work done by the gas on the right part? (b) Find the final pressures on the two sides. (c) Find the final equilibrium temperature. (d) How much heat has flown from the gas on the right to the gas on the left?

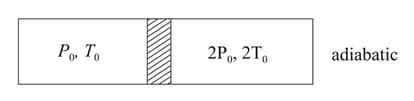
An ideal gas $\left(\frac{C_p}{C_v}=\gamma \right)$ having initial pressure $P_0$ and volume $V_0$.

(a) The gas is taken isothermally to a pressure $2P_0$ and then adiabatically to a pressure $4P_0$. Find the final volume.

(b) The gas is brought back to its initial state. It is adiabatically taken to a pressure $2P_{0 }$and then isothermally to a pressure $4P_0$. Find the final volume.

Two samples $A$ and $B$ of the same gas have equal volumes and pressures. The gas in sample $A$ is expanded isothermally to four times of its initial volume and the gas in $B$ is expanded adiabatically to double of its volume. If works done in isothermal process is twice that of adiabatic process, then show that $\gamma$ satisfies the equation $1 – 2^{\left(1–\gamma \right)}=(\mathrm{\gamma }–1)\mathrm{In}2.$

A Carnot engine cycle is shown in the figure (2). The cycle runs between temperatures$T_H=\alpha T_0 \text{and }{T}_L=T_0 (\alpha > 1).$ Minimum and maximum volume at state $1$ and state $3$ are ${\mathrm{V}}_0$ and $n{V}_0$, respectively. The cycle uses one mole of an ideal gas with $\frac{{\mathit{C}}_{\mathit{P}}\mathit{ }}{{\mathit{C}}_{\mathit{V}}}=\mathrm{\gamma }$. Here $C_P$and $C_V$ are the specific heats at constant pressure and volume respectively. You must express all answers in terms of the given parameters  $\left\{\alpha ,n,T_0,V_0\right\},?$ and universal gas constant $R$.

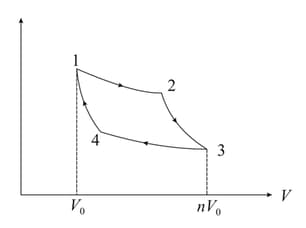
(a) Find $P, V, T$ for all the states

(b) Calculate the work done by the engine in each process $W_{12}, W_{23}, W_{34}, W_{41}.$

(c) Calculate $Q$, the heat absorbed in the cycle.

Cloud formation condition

Consider a simplified model of cloud formation. Hot air in contact with the earth’s surface contains water vapour. This air rises connectively till the water vapour content reaches its saturation pressure. When this happens, the water vapour starts condensing and droplets are formed. We shall estimate the height at which this happens. We assume that the atmosphere consists of the diatomic gases oxygen and nitrogen in the mass proportion $21:79$ respectively. We further assume that the atmosphere is an ideal gas, $g$ the acceleration due to gravity is constant and air processes are adiabatic. Under these assumptions one can show that the pressure is given by

$p=p_0{\left(\frac{T_0-\tau Z}{T_0}\right)}^{\alpha }$

Here $p_0$ and $T_0$ is the pressure and temperature respectively at sea level $(\mathrm{z} = 0), \tau$ is the lapse rate (magnitude of the change in temperature $T$ with height $z$ above the earth’s surface, i.e. $\tau > 0$).

(a) Obtain an expression for the lapse rate $\mathrm{\Gamma }$ in terms of $\gamma , R, g$ and $m_a$. Here $\mathrm{\gamma }$ is the ratio of specific heat at constant pressure to specific heat at constant volume; $R$, the gas constant; and $m_a$, the relevant molar mass. 

(b) Estimate the change in temperature when we ascend a height of one kilometre ?

(c) Show that pressure will depend on height as given by Eq. (1). Find an explicit expression for exponent $\mathrm{\alpha }$ in terms of $\mathrm{\gamma }$.

(d) According to this model what is the height to which the atmosphere extends? Take $T_0 = 300 \mathrm{K}$and $p_0 = 1 \mathrm{atm}.$