Embibe Experts Solutions for Chapter: Wave Motion on a String, Exercise 4: Exercise - 4
Embibe Experts Physics Solutions for Exercise - Embibe Experts Solutions for Chapter: Wave Motion on a String, Exercise 4: Exercise - 4
Attempt the free practice questions on Chapter 20: Wave Motion on a String, Exercise 4: Exercise - 4 with hints and solutions to strengthen your understanding. Alpha Question Bank for Engineering: Physics solutions are prepared by Experienced Embibe Experts.
Questions from Embibe Experts Solutions for Chapter: Wave Motion on a String, Exercise 4: Exercise - 4 with Hints & Solutions
Two transverse sine waves each of amplitude wavelength and time period and in phase at are travelling along the -axis in opposite direction. Obtain the equation of the resultant wave and comment on its nature calculate the maximum displacement at Also locate the antinodes and nodes.
A tube long is closed at one end. A wire of lengthand mass is stretched between two fixed ends and is placed near the open end. When the wire is plucked at its mid point the air column resonates in itsovertone. Find the tension in the wire if it vibrates in its fundamental mode.
A point isotropic sound source is located on the perpendicular to the plane of a ring, drawn through the centre of the ring. The distance between the point and the source is and the radius of the ring is . Find the mean energy flow across the area enclosed by the ring, if at point , the intensity of sound is equal to . The damping of the waves is negligible.
A guitar string is long and has a fundamental frequency of . Where should it be pressed to produce a fundamental frequency of ?
A piano wire weighing and having a length of emits a fundamental frequency corresponding to the “Middle ” . Find the tension in the wire.
The length of a sonometer wire is . Find the length of the three segments for fundamental frequencies to be in the ratio .
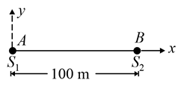
In the figure shown and are two ends of a string of length and are two sources due to which points and oscillate in and directions respectively according to the equation and where is in and is in . The speed of propagation of disturbance along the string is . Find the instantaneous position vector (in ) and velocity vector in of a particle of string which is at from . You have to find these parameters after both the disturbances from and have reached . Also find the phase difference between the waves at the point when they meet at first time.
A string of mass is fixed at both ends. The fundamental tone oscillations are excited with angular frequency and maximum displacement amplitude . Find:
(a) the maximum kinetic energy of the string;
(b) the mean kinetic energy of the string averaged over one oscillation period.
