Embibe Experts Solutions for Chapter: Kinetic Theory of Gases, Exercise 2: Exercise-2

An ideal gas is initially at temperature $T$ and volume $V.$ Its volume is increased by $\Delta V$ due to an increase in temperature $\Delta T,$ pressure remaining constant. The quantity $\delta \mathit{=}\frac{\mathit{\Delta }\mathit{V}}{\mathit{V}\mathit{\Delta }\mathit{T}}$ varies with temperature as: 

Which of the following graphs correctly represents the variation of $\beta =\frac{-\left({\displaystyle \frac{dV}{dP}}\right)}{N}$ with $P$ for an ideal gas at constant temperature? 

One mole of a monatomic ideal gas is taken along two cyclic processes $E\mathit{\to }F\mathit{\to }G\mathit{\to }E$ and $E\mathit{\to }F$ $\to H\to E$ as shown in the $PV$ diagram. The processes involved are purely isochoric, isobaric, isothermal or adiabatic.

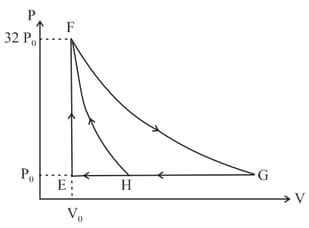
Match the paths in List I with the magnitudes of the work done in List II and select the correct answer using the codes given below the lists. 

Assertion: The root mean square velocity of molecules of a gas having Maxwellian distribution of velocities is higher than their most probable velocity at any temperature.

Reason: A very small number of molecules of a gas possessing very large velocities increases the root mean square velocity without affecting the most probable velocity.

Assertion: Two different gases having same temperature always have molecules with same RMS
speed.

Reason: The average translational kinetic energy per mole for each gas is $\frac{3}{2}KT$ (where, $K=$Boltzmann constant, $T=$temperature in Kelvin).

Assertion: The pressure of a gas filled in a cylinder fitted with an immovable piston is increased by raising its temperature.

Reason: On raising the temperature, greater momentum is transferred to the wall of the container per second.

Assertion: It is possible for both the pressure and volume of a monoatomic ideal gas of a given amount to change simultaneously without causing the internal energy of the gas to change.

Reason: The internal energy of an ideal gas of a given amount remains constant if temperature does not change. It is possible to have a process in which pressure and volume are changed such that temperature remains constant.

Assertion: Equal moles of helium and oxygen gases are given equal quantities of heat at constant volume. There will be a greater rise in the temperature of helium as compared to that of oxygen.

Reason: The molecular weight of oxygen is more than the molecular weight of helium.