Embibe Experts Solutions for Chapter: Rotational Mechanics, Exercise 3: Exercise-3
Embibe Experts Physics Solutions for Exercise - Embibe Experts Solutions for Chapter: Rotational Mechanics, Exercise 3: Exercise-3
Attempt the practice questions on Chapter 10: Rotational Mechanics, Exercise 3: Exercise-3 with hints and solutions to strengthen your understanding. Alpha Question Bank for Medical: Physics solutions are prepared by Experienced Embibe Experts.
Questions from Embibe Experts Solutions for Chapter: Rotational Mechanics, Exercise 3: Exercise-3 with Hints & Solutions
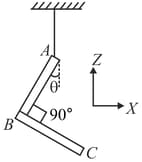
An L-shaped object made of thin rods of uniform mass density is suspended with a string as shown in figure. If and the angle made by with downward vertical is , then,
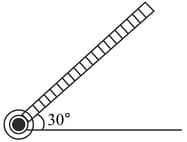
A rod of length is pivoted at one end. It is raised such that if makes an angle of from the horizontal as shown and released from rest. Its angular speed when it passes through the horizontal (in ) will be
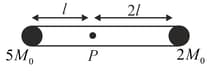
A rigid massless rod of length has two masses attached at each end as shown in the figure. The rod is pivoted at point on the horizontal axis (see figure). When released from the initial horizontal position, its instantaneous angular acceleration will be:
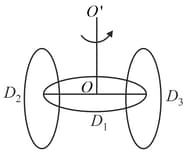
A circular disc of mass and radius has two identical discs and of the same mass and radius attached rigidly at its opposite ends (see figure.) The moment of inertia of the system about the axis , passing through the centre of as shown in the figure, will be:
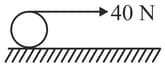
A string is wound around a hollow cylinder of mass and radius . If the string is now pulled with a horizontal force of , and the cylinder is rolling without slipping on a horizontal surface (see figure), then the angular acceleration of the cylinder will be (Neglect the mass and thickness of the string):
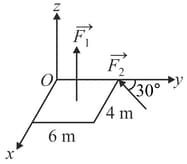
A slab is subjected to two forces and of the same magnitude as shown in the figure. Force is in -plane while force acts along the axis at the point . The moment of these forces about point will be
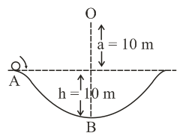
A particle of mass is released with an initial velocity along the curve from the point , as shown in figure. The point is at height from point . The particle slides along the frictionless surface. When the particle reaches point , its angular momentum about will be
The moment of inertia of a solid sphere, about an axis parallel to its diameter and at a distance of from it is . Which one of the graphs represents the variation of with correctly?
