Embibe Experts Solutions for Chapter: Application of Derivatives, Exercise 3: EXERCISE-3

Positive integral value of $\text{'}a\text{'}$ for which the function $f\left(x\right)=x^3+\left(2a+3\right)x^2+3\left(2a+1\right)x+5$ is monotonic in $R,$ is

Largest value of $f\left(x\right)=12x^{4/3}-6x^{1/3}, x\in \left[-1, 1\right]$ is equal to

Maximum value of $f\left(x\right)=4x-\frac{x^2}{2}; x\in \left[-2,\frac{9}{2}\right]$ is

Maximum value of $f\left(x\right)=3x^4-8x^3+12x^2-48x+25; x\in \left[0, 3\right]$ is

Maximum value of $f\left(x\right)=\sin x+\frac{1}{2}\cos 2x; x\in \left[0,\frac{\pi }{2}\right]$ is

Let $x$ and $y$ be two real variable such that $x>0$ and $xy=1$. Find the minimum value of $x+y$.

The flower bed is to be in the shape of a circular sector of radius $r$ and central angle $\theta$. If the area is fixed & perimeter is minimum, then value of $\theta$ is

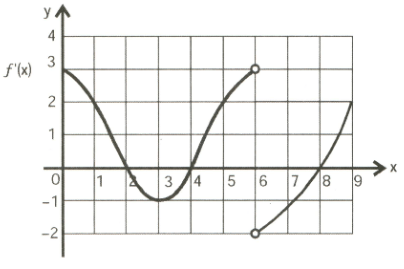
The graph of the derivative $f^{\text{'}}$ of a continuous function $f$ is shown with $f\left(0\right)=0.$ If

(i) $f$ is monotonic increasing in the interval $\left[a, b\right)\cup \left(c, d\right)\cup \left(e, f\right]$ and decreasing in $\left(p, q\right)\cup \left(r, s\right)$.

(ii) $f$ has local minima at $x=x_1$and $x=x_2$.

(iii) $f$ is concave up in $\left(\mathcal{l}, m\right)\cup \left(n, t\right]$.

(iv) $f$ has inflection point at $x=k$.

(v) number of critical points of $y=f\left(x\right)$ is $\text{'}w\text{'}$.

The value of $\left(a+b+c+d+e\right)+\left(p+q+r+s\right)+\left(\mathcal{l}+m+n\right)+\left(x_1+x_2\right)+\left(k+w\right)$ is