Embibe Experts Solutions for Chapter: Circular Motion, Exercise 2: Exercise-2

A particle moves with deceleration along the circle of radius $R$ so that at any moment of time its tangential and the speed of the particle as a function of the distance covered $S$ will be 

A particle moves along an arc of a circle of radius $R$. Its velocity depends on the distance covered $s$ as $v=a\sqrt{s}$, where $a$ is a constant then the angle $\alpha$ between the vector of the total acceleration and the vector of velocity as a function of $s$ will be

A particle is moving along the circle $x^2+y^2=a^2$ in anticlockwise direction. The $x-y$ is a rough horizontal stationary surface. At the point $\left(a\cos \theta , a\sin \theta \right)$, the unit vector in the direction of friction on the particle is

A car runs around a curve of radius $10 \mathrm{m}$ at a constant speed of $10 {\mathrm{ms}}^{-1}$. Consider the time interval for which car covers a curve $120 ° \mathrm{arc}$

A car is moving with constant speed on a rough banked road.

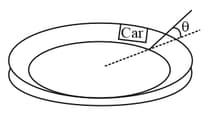
Figure shows the free body diagram of car in three situation $A, B$ and $C$ respectively.

A cube of mass $M$ starts at rest from point $1$ at a height $4\mathrm{R}$, where $R$ is the radius of the circular track. The cube slides down the frictionless track and around the loop. The force which the track exerts on the cube at point $2$ is:

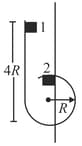
A collar $\text{'}B\text{'}$ of mas $2\mathrm{kg}$ is constrained to move along a horizontal smooth and fixed circular track of radius $5\mathrm{m}.$ The spring lying in the plane of the circular track and having spring constant $200N/m$ is undeformed when the collar is at $\text{'}A\text{'}$. If the collar start form rest at $\text{'}B\text{'}$ the normal reaction exerted by the track on the collar when is passes through $\text{'}A\text{'}$ is:

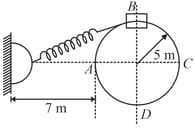
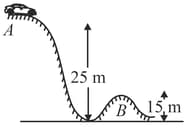
Figure shown the roller coaster track. Each car will start from rest at point $A$ and will roll with negligible friction. If is important that there should be at least some small positive normal force exerted by the track on the car at all points, otherwise the car would leave the track. With the above fact, the minimum safe value for the radius of curvature at point $B$ is $\left(g=10{\mathrm{ms}}^2\right):$