Embibe Experts Solutions for Chapter: Circular Motion, Exercise 4: Exercise-4

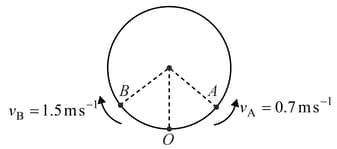
Two particles $A$ and $B$ start at $O$ and travel in opposite direction along the circular path at constant speed $v_A=0.7{\mathrm{ms}}^{-1}$ and$v_A=1.5{\mathrm{ms}}^{-1}$ respectively. Determine the when they collide and the magnitude of the acceleration of $B$ just before this happening.(radius=$5\mathrm{m}$)

A particle is moving in a circular orbit with a constant tangential acceleration. After a certain time $t$ has elapsed after the beginning of motion, the angle between the total acceleration a and the direction along the radius $r$ becomes equal to $45°.$ What is the angular acceleration of the particle.

Two particles $A$ and $B$ move anticlockwise with the same speed $v$ in a circle of radius $R$ and are diametrically opposite to each other.At $t=0, A$ is given a constant acceleration (tangential) $a_t=\frac{72v^2}{25\mathrm{\pi R}}.$calculate the time in which $A$ collides with $B$, The angle traced by $A$,its angular velocity and radial acceleration at the time of collision.

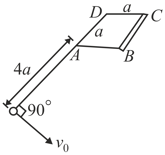
A square plate is firmly attached to a frictionless horizontal plane. One end of a taut cord is attached to point $A$ of the plate and he cord gets wrapped around the plate. The sphere is given an initial velocity $v_0$ on the horizontal plane perpendicular to the cord which causes it to make a complete circle of the plate and return to point $A$. Find the velocity of the sphere when it hits point $A$ again after moving in a circle on the horizontal plane. Also find the time taken by the sphere to complete the circle.

Starting from rest, a particle rotates in a circle of radius $R=\sqrt{2} \mathrm{m}$ with an angular acceleration $\alpha =\frac{\pi }{4}\mathrm{rad} {\sec }^2$. Calculate the magnitude of average velocity of the particle over the time it rotates quarter circle.

A stone weighing $0.5 \mathrm{kg}$ tied to a rope of length $0.5 \mathrm{m}$ revolves along a circular path in a vertical plane. The tension of the rope at the bottom point of the circle is $45 \mathrm{N}$. To what height will the stone rise if the rope breaks at the moment when the velocity is directed upwards? $(g=10 \mathrm{m} {\mathrm{s}}^{-2})$

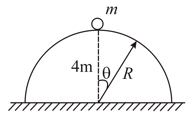
A hemisphere of radius $R$ and of mass $4 m$ is free to slide with its base on a smooth horizontal table. A particle of mass $m$ is placed on the top of the hemisphere. Find the angular velocity of the particle relative to hemisphere an angular displacement $\theta$ when velocity of hemisphere has become $v$.