Embibe Experts Solutions for Chapter: Dual Nature of Matter and Radiation, Exercise 4: Exercise-4
Embibe Experts Physics Solutions for Exercise - Embibe Experts Solutions for Chapter: Dual Nature of Matter and Radiation, Exercise 4: Exercise-4
Attempt the free practice questions on Chapter 32: Dual Nature of Matter and Radiation, Exercise 4: Exercise-4 with hints and solutions to strengthen your understanding. Beta Question Bank for Engineering: Physics solutions are prepared by Experienced Embibe Experts.
Questions from Embibe Experts Solutions for Chapter: Dual Nature of Matter and Radiation, Exercise 4: Exercise-4 with Hints & Solutions
A monochromatic point source S radiating wavelength with power watt, an aperture of diameter a large screen are placed as shown in figure. A photoemissive detector D of surface area is placed at the centre of the screen. The efficiency of the detector for the photoelectron generation per incident photon is
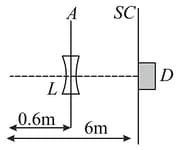
(i) Calculate the photon flux density at the centre of the screen and the photo current in the detector.
(ii) If a concave lens of focal length is inserted in the aperture as shown, find the new values of photon flux density & photocurrent. Assume a uniform average transmission of for the lens.
(iii) If the work-function of the photoemissive surface is , calculate the values of the stopping potential in the two cases (without & with the lens in the aperture).
A beam of light has three wavelengths with a total intensity equally distributed amongst the three wavelength. The beam falls normally on an area of clean metallic surface of work function . Calculate photo current. (Assume each energetically suitable photon emits one electron)
Two identical non-relativistic particles move at right angles to each other, possessing de Broglie wavelengths and Find the de Broglie wavelengths of each particle in the frame of their centre of inertia.
