Embibe Experts Solutions for Chapter: Electromagnetic Induction, Exercise 2: Exercise-2

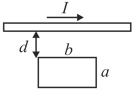
$PQ$ is an infinite current carrying conductor. $AB$ and $CD$ are smooth conducting rods on which a conductor $EF$ moves with constant velocity $V$ as shown. The force needed to maintain constant speed of $EF$ is

Two different coils have self-inductances $L_1=8\mathrm{mH}$ and $L_2=2\mathrm{mH}$. The current in one coil is increased at a constant rate. The current in the second coil is also increased at the same constant rate. At a certain instant of time, the power given to the two coils is the same. At that time, the current, the induced voltage and the energy stored in the first coil are $i_1,{ V}_1$ and $W_1$ respectively. Corresponding values for the second coil at the same instant are $i_2,{ V}_2$ and $W_2$ respectively. Then:

An electron is moving in a circular orbit of radius$R$ with an angular acceleration $\alpha$. At the centre of the orbit is kept a conducting loop of radius $r,(r<<R)$. The e.m.f. induced in the smaller loop due to the motion of the electron is

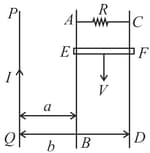
A long straight wire is parallel to one edge as in figure. If the current in the long wire is varies in time as $I=I_0{e}^{\frac{-t}{\tau }}$, what will be the induced emf in the loop?

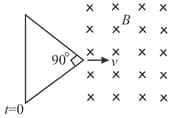
The figure shows an isosceles triangle wire frame with apex angle equal to $\frac{\pi }{2}$. The frame starts entering into the region of uniform magnetic field $B$ with constant velocity $v$ at $t=0$. The longest side of the frame is perpendicular to the direction of velocity. If $i$ is the instantaneous current through the frame then choose the alternative showing the correct variation of $i$ with time.

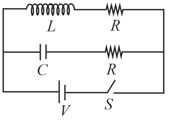
The frequency of oscillation of current in the inductor is

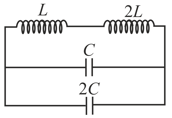
At a moment $\left(t=0\right)$ when charge on capacitor $C_1$ is zero, the switch is closed. If $I_0$ be the current through inductor at that instant, for $t>0$,

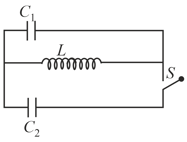
In the circuit shown in the figure, $R=\sqrt{\frac{L}{C}}$. Switch $S$ is closed at time $t=0$. The current through $C$ and $L$ would be equal after a time $t$ equal to