Embibe Experts Solutions for Chapter: Electrostatics, Exercise 3: Exercise-3

Consider three identical metal spheres $A,B$ and $C$. Spheres A carries charge $+6q$ and sphere $B$ carries charge $-3q$. Sphere $C$ carries no charge. Spheres $A$ and $B$ are touched together and then separated. Sphere $C$ is then touched to sphere $A$ and separated from it. Finally the sphere $C$ is touched to sphere $B$ and separated from it. If the final charge on the sphere $C$ is $nq$, find $n$.

The escape speed of an electron launched from the surface of a $1 \mathrm{cm}$ diameter glass sphere that has been charged to $10 \mathrm{nC}$ is........ $\times {10}^7 \mathrm{m} {\sec }^{-1}$. (Round off to the nearest integer)

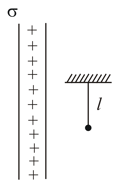
A simple pendulum of length $\ell$ and bob mass $m$ is hanging in front of a large nonconducting sheet having surface charge density $\sigma$. If suddenly a charge $+q$ is given to the bob \& it is released from the position
shown in figure. If the maximum angle through which the string is deflected from vertical is $x{\tan }^{-1}\left(\frac{\sigma q_{\mathit{0}}}{2{\epsilon }_{0}mg}\right)$, then find $x$.

Two fixed, equal, positive charges, each of magnitude $q=5\times {10}^{-5} \mathrm{C}$ are located at points $A$ and $B$ separated by a distance of $6 \mathrm{m}$. An equal and opposite charge moves towards them along the line $\mathrm{COD}$, the perpendicular bisector of the line $AB$. The moving charge, when it reaches the point $C$ at a distance of $4 \mathrm{m}$ from $O$, has a kinetic energy of $4 \mathrm{J}$. Calculate the distance of the farthest point $D$ (in meter) which the negative charge will reach before returning towards $C$.

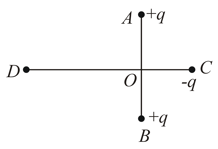
Two point dipoles $p\hat{k}$ and $\frac{P}{2}\hat{k}$ are located at $\left(0,0,0\right)$ and $\left(1 m, 0, 2 m\right)$ respectively. If the resultant electric field due to the two dipoles at the point $\left(1 m, 0, 0\right)$ is $\frac{-7}{x}kP\hat{\mathit{k}}$, find $x$.

The length of each side of a cubical closed surface is $\ell$. If charge $q$ is situated on one of the vertices of the cube, then if the flux passing through shaded face of the cube is $\frac{q}{3n{\epsilon }_0}$, find the value of $n$.

A charge $Q$ is uniformly distributed over a rod of length $\ell$. Consider a hypothetical cube of edge $\ell$ with the centre of the cube at one end of the rod. If the minimum possible flux of the electric field through the entire surface of the cube is $\frac{Q}{x{\epsilon }_0}$, find $x$.

There are $27$ drops of a conducting fluid. Each has a radius $r$ and they are charged to a potential $V_0$. They are then combined to form a bigger drop. If the potential of bigger drop is n $V_0$ then find $n$.