Embibe Experts Solutions for Chapter: Gravitation, Exercise 3: Exercise-3

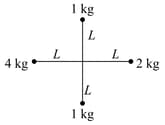
In the given figure, $L=1\mathrm{m}$, if total gravitational force on $4 \mathrm{kg}$ mass is ${\overrightarrow{\mathrm{F}}}_1$ and on $2 \mathrm{kg}$ mass is${\overrightarrow{\mathrm{F}}}_2$, If the value of the ratio of $\left|\frac{{\overrightarrow{\mathrm{F}}}_1}{{\overrightarrow{\mathrm{F}}}_2}\right|$ is $\sqrt{\alpha }$, then what will be the value of $\alpha ?$

Two point-like objects, each with mass $m$ , are connected by a massless rope of length $l$ . The objects are suspended vertically near the surface of Earth, so that one object is hanging below the other. Then the objects are released. If the tension in the rope is $T=\frac{GMml}{R^x}$, where $M$ is the mass of the Earth and $R$ is its radius $\left[l\ll \mathrm{R}\right]$, then find value of $x$ . 

A solid sphere of uniform density and radius $R$ applies a gravitational force of attraction equal to $F_1$ on a particle placed at $P$, distance $2R$ from the centre of the sphere. A spherical cavity of radius $\frac{R}{2}$ is now made in the sphere as shown in figure. The sphere with cavity now applies a gravitational force $F_2$ on the same particle placed at $P.$ If the value of the ratio of $\frac{F_2}{F_1}$ is $\frac{7}{\alpha }$, then find $\alpha$ .

The gravitational field in a region is given by $\overrightarrow{E}=\left(3\hat{\mathrm{i}}-4\hat{\mathrm{j}}\right) \mathrm{N} {\mathrm{kg}}^{-1}$ . Find out the work done (in joule) in displacing a particle by $1 \mathrm{m}$ , along the line $4y=3x+9$.

The Earth may be regarded as a spherically shaped uniform core of density ${\rho }_1$  and radius $\frac{R}{2}$  surrounded by a uniform shell of thickness $\frac{R}{2}$ and density ${\rho }_2$ . If the ratio of $\frac{{\rho }_1}{{\rho }_2}$ is $\frac{7}{x}$, then find the value of $x$. It is given that the value of acceleration due to gravity is the same at surface as at depth $\frac{R}{2}$ from the surface.

A thin spherical shell of total mass$M$  and radius$R$  is held fixed. There is a small hole in the shell. A mass$m$  is released from rest a distance $\mathrm{R}$ from the hole along a line that passes through the hole and also through the centre of the shell. This mass subsequently moves under the gravitational force of the shell. If mass takes time  $t=\alpha \sqrt{\frac{R^3}{GM}}$, to travel from the hole to the point diametrically opposite. Find the value of $\alpha$. Consider all units in SI system.

A particle of mass $1 \mathrm{kg}$  is placed at a distance of$4 \mathrm{m}$  from the centre and on the axis of a uniform ring of mass $5 \mathrm{~kg}$, and radius $3 \mathrm{~m}$. The work done to increase the distance of the particle from $4 \mathrm{~m}$ to $3 \sqrt{3} \mathrm{~m}$ is $\alpha \times 10^{-11}$ Joule, then the value $\alpha$ is

The minimum and maximum distances of a satellite from the centre of the Earth are $2R$  and $4R$  respectively, where, $R$  is the radius of Earth and $M$ is the mass of the Earth. Radius of curvature at the point of minimum distance is$\frac{\alpha R}{3}$ , then the value of $\alpha$ is,