Embibe Experts Solutions for Chapter: Gravitation, Exercise 4: Exercise-4

A body moving radially away from a planet of mass$\mathrm{M}$, when at distance $\mathrm{r}$ from planet, explodes in such a way that two of its many fragments move in mutually perpendicular circular orbits around the planet. What will be

(i) Then velocity in circular orbits?
(ii) Maximum distance between the two fragments before collision and
(iii) Magnitude of their relative velocity just before they collide?

The fastest possible rate of rotation of a planet is that for which the gravitational force on material at the equator barely provides the centripetal force needed for the rotation. (Why?) 

(i) Show then that the corresponding shortest period of rotation is given by $\mathrm{T}=\sqrt{\frac{3\pi }{\mathrm{Gp}}}$ where $\rho$ is the density of the planet, assumed to be homogeneous.

(ii) Evaluate the rotation period assuming a density of $3.0\mathrm{gm} {\mathrm{cm}}^{-3}$ typical of many planets, satellites, and asteroids. No such object is found to be spinning with a period shorter than found by this analysis.

In a particular double star system, two stars of mass $3.22\times {10}^{30} \mathrm{kg}$ each revolve about their common centre of mass, $1.12\times {10}^{11} \mathrm{m}$ away.

(i) Calculate their common period of revolution, in years.

(ii) Suppose that a meteoroid (small solid particle in space) passes through this centre of mass moving at right angles to the orbital plane of the stars. What must its speed be if it is to escape from the gravitational field of the double star?

Consider two satellites $A$ and $B$ of equal mass $m$, moving in the same circular orbit of radius $r$ around the Earth $E$ but in opposite sense of rotation and therefore on a collision course (see figure).

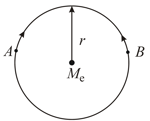
In terms of $G,M_e,m$ and $r$ the total mechanical energy $E_A+E_B$ of the two satellite plus Earth system before collision is given by$\frac{-\beta G{\mathrm{mM}}_e}{r}$ then find the value of $\beta$ .

Consider two satellites $A$ and $B$ of equal mass $m$, moving in the same circular orbit of radius $r$ around the Earth $E$ but in opposite sense of rotation and therefore on a collision course (see figure).

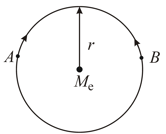
If the collision is completely inelastic so that wreckage remains as one piece of tangled material (mass $=\mathit{2}m$), the total mechanical energy immediately after collision is given by $-\frac{a{\mathrm{GmM}}_e}{\mathrm{r}}$. Find $a$.

Consider two satellites $A$ and $B$ of equal mass $m$, moving in the same circular orbit of radius $r$ around the Earth $E$ but in opposite sense of rotation and therefore on a collision course (see figure).

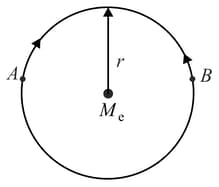
Describe the subsequent motion of the wreckage.

A body of mass $m$ be projected vertically upward from the surface of the Earth so as to reach a height $nR$ above the Earth's surface. If the increase in its potential energy is $∆\mathrm{U}=\frac{\mathrm{GMm}}{\mathrm{R}}\left(\frac{\mathrm{\alpha }}{1+\mathrm{\beta }}\right)$, find $\alpha -\beta$ .

A body of mass $m$ be projected vertically upward from the surface of the Earth so as to reach a height $nR$ above the Earth's surface. If the velocity with which the body must be projected is given by $\sqrt{\frac{\alpha GM}{R}\left(\frac{1}{1+n}\right)}$, then find value of $\alpha$.