Embibe Experts Solutions for Chapter: Laws of Motion, Exercise 4: Exercise-4

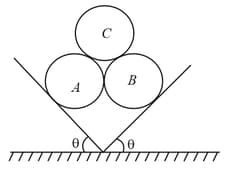
Three identical rigid cylinders $A,B$ and $C$ are arranged on smooth inclined surfaces as shown in figure. Find the least value of $\theta$ that prevent the arrangement from collapse.

Block $C$ descends vertically at $1 {\text{m s}}^{-1}$. Find the velocity of $A$ relative to $B$.

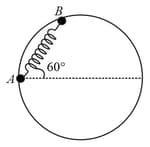
A bead of mass $m$ is attached to one end of a spring of natural length $\sqrt{3}\mathrm{R}$ and spring constant $k=\frac{\left(\sqrt{3}+1\right)\mathrm{mg}}{R}$. The other end of the spring is fixed at point $A$ on a smooth fixed vertical ring of radius $R$ as shown in the figure. What is the normal reaction at $B$ just after the bead is released?

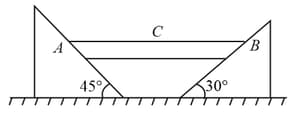
The blocks are of mass $\text{2 kg}$ shown is in equilibrium. At $t=0$ right spring in figure(i) and right string in figure (ii) breaks. Find the ratio of instantaneous acceleration of blocks?

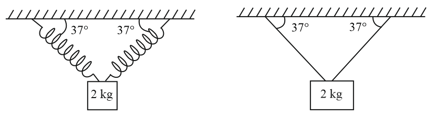
Fig. shows a bead of mass $m$ moving with uniform speed $v$ through a U-shaped smooth wire the wire has a semicircular bending between $A$ and $B$. Calculate the average force exerted by the bead on the part $AB$ of the wire.

A monkey of mass, $40 \mathrm{kg}$ climbs on a rope that can stand a maximum tension of $600 \mathrm{N}$. Calculate the tension in rope in the following cases. In which case will the rope break:

(i) The monkey climbs up with an acceleration of $6 \mathrm{m} {\mathrm{s}}^{-2}$

(ii) The monkey climbs down with an acceleration of $4 \mathrm{m} {\mathrm{s}}^{-2}$

(iii) The monkey climbs up with a uniform speed of, $5 \mathrm{m} {\mathrm{s}}^{-1}$. Neglect the mass of string. 

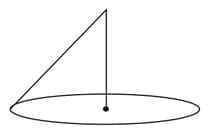
Consider a conical pendulum having a bob of mass, $m$ is suspended from a ceiling through a string of length, $L$. The bob moves in a horizontal circle of radius, $r$. Find (a) the angular speed of the bob and (b) the tension in the string.

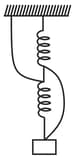
In figure two identical springs, each with a relaxed length of $50 \mathrm{cm}$ and a spring constant of $500 {\mathrm{Nm}}^{-1}$, are connected by a short cord of length $10 \mathrm{cm}$. The upper string is attached to the ceiling, a box that weighs $100\mathrm{N}$ hangs from the lower spring. Two additional cords, each $85 \mathrm{cm}$ long, are also tied to the assembly; they are limp (i.e,slack).

(i) If the short cord is cut, so that the box then hangs from the springs and the two longer cords, does the box move up or down?

(ii) How far does the box move before coming to rest again?