Embibe Experts Solutions for Chapter: Simple Harmonic Motion, Exercise 4: Exercise-4

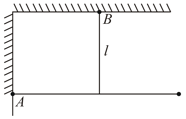
A weightless rigid rod with a load at the end is hinged at point $A$ to the wall so that it can rotate in all directions. The rod is kept in the horizontal position by a vertical inextensible thread of length $\mathcal{l}$, fixed at its midpoint. The load receives a momentum in the direction perpendicular to the plane of the figure. Determine the period $T$ of small oscillations of the system.

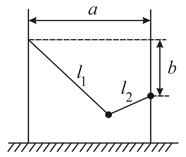
One rope of a swing is fixed above the other rope by $b$. The distance between the poles of the swing is $a$. The lengths ${\mathcal{l}}_1$ and ${\mathcal{l}}_2$ of the ropes are such that ${\mathcal{l}}_1^2+{\mathcal{l}}_2^2=a^2+b^2$. (Fig.) Determine the period $T$ of small oscillations of the swing, neglecting the height of the swining person in comparison with the above lengths. 

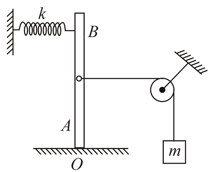
A massless road rigidly fixed at $O$. A string carrying a mass $m$ at one end is attached to point $A$ on the rod so that $OA=a$. At another point $B\left(OB=b\right)$ pf the rod, a horizontal spring of force constant $k$ is attached as shown. Find the period of small vertical oscillations of mass $m$ around its equilibrium position

A life operator hung an exact pendulum clock on the lift wall in a lift in a building to know end of the working day. The lift moves with an upward & downward accelerations during the same time (according to a stationary clock), the magnitudes of the acceleration remaining unchanged. Will the operator work for more or less than required time.

In the figure shown, the spring are connected to the rod at one end and at the midpoint. The rod is hinged at its lower end.

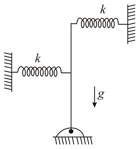
(i) Find the minimum value of $k$ for rotational $\mathrm{SHM}$ of the rod (Mass $m$, length $L$)

(ii) If $k=\mathrm{mg} {\mathrm{L}}^{-1}$ then find the angular frequency of oscillations of the rod.

Two identical balls $A$ and $B$ each of mass $0.1 \mathrm{kg}$ are attached to two identical massless springs. The spring mass system is constrained to move inside a rigid smooth pipe in the form of a circle as in fig. The pipe is fixed in a horizontal plane. The centres of the ball can move in a circle of radius $0.06 \mathrm{m}$. Each spring has a natural length $0.06 \mathrm{\pi m}$ and force constant $0.1 \mathrm{N} {\mathrm{m}}^{-1}$. Initially both the balls are displaced by an angle of $\theta =\pi /6$ radian with respect to diameter $PQ$ of the circle and released from rest

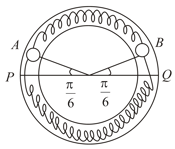
(i) calculate the frequency of oscillation of the ball $B$.

(ii) what is the total energy of the system

(iii) find the speed of the ball $A$ when $A$ and $B$ are at the two ends of the diameter $PQ$. 

A rod of mass $M$ and length $L$ is hinged at its one end and carries a block of mass $m$ at its other end. $A$ spring of force constant $k_1$ is installed at distance a from the hinge and another of force constant $k_2$ at a distance $b$ as shown in the figure. If the whole arrangement rests on a smooth horizontal table top. find the frequency of vibration.

The following equation represent transverse wave;

$z_1=A\cos \left(kx-\omega t\right),z_2=A\cos \left(kx+\omega t\right),z_3=A\cos \left(ky-\omega t\right)$

Identify the combination (s) of the waves which will produce. (i) standing wave (s) (ii) a wave travelling in the direction making an angle of $45°$ with the positive $x$ and positive $y$-axis. In each case, find the position at which the resultant intensity is always zero.