Embibe Experts Solutions for Chapter: Rotational Mechanics, Exercise 3: BEGINNER'S BOX - 3

Two rings having the same radius and mass are placed such that their centres are at a common point and their planes are perpendicular to each other. Find the moment of inertia of the system about an axis passing through the centre and perpendicular to the plane of one of the rings. ($M=$mass of each ring and $R=$ radius).

Moment of inertia of a sphere about its diameter is $\frac{2}{5}M{R}^2$. What is its moment of inertia about an axis perpendicular to its two diameters and passing through their point of intersection?

A force $\overrightarrow{F}=(\hat{\mathrm{i}}-2\hat{\mathrm{j}}+5\hat{\mathrm{k}}) \mathrm{N}$ is acting at a point $\overrightarrow{r}=(2\hat{\mathrm{i}}+\hat{\mathrm{j}}+3\hat{\mathrm{k}}) \mathrm{m}$. Find torque about the origin.

The density of a rod $AB$ increases continuously from $A$ to $B$. Is it easier to set it in rotation by clamping it at $A$ and applying a perpendicular force at $B$ or by clamping it at $B$ and applying the force at $A$? Explain your answer.

A uniform disc of radius $20 \mathrm{cm}$ and mass $2 \mathrm{kg}$ can rotate about a fixed axis through the centre and perpendicular to its plane. A massless cord is round along the rim of the disc. If a uniform force of $2 \mathrm{newtons}$ is applied on the cord, tangential acceleration of a point on the rim of the disc will be

A door $1.6 \mathrm{m}$ wide requires a minimum force of $1 \mathrm{N}$ to be applied at the free end to open or close it. The minimum force that is required at a point $0.4 \mathrm{m}$ away from the hinges for opening or closing the door is

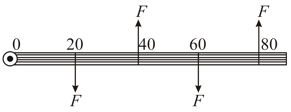
Four equal and parallel forces are acting on a rod (as shown in figure at distances of $20 \mathrm{cm}$, $40 \mathrm{cm}$, $60 \mathrm{cm}$ and $80 \mathrm{cm}$ respectively from one end of the rod. Under the influence of these forces the rod

A weightless rod is acted on by upward parallel forces of $2 \mathrm{N}$ and $4 \mathrm{N}$ at ends $\mathrm{A}$ and $\mathrm{B}$, respectively. The total length of the rod is $\mathrm{AB}=3 \mathrm{m}$. To keep the rod in equilibrium, a force of $6 \mathrm{N}$ should act in the following manner: