Embibe Experts Solutions for Chapter: Triangle, Exercise 1: IOQM - PRMO and RMO 2018

If $ABCD$ is a rectangle and $P$ is a point inside it such that $AP=33, BP=16, DP=63.$ Find $CP.$

Let $ABC$ be an equilateral triangle with side length $10.$ A square $PQRS$ is inscribed in it, with $P$ on $AB. Q, R$ on $BC$ and $S$ on $AC.$ If the area of the square $PQRS$ is $m+n\sqrt{k}$ where $m, n$ are integers and $k$ is a prime number then determine the value of $\sqrt{\frac{m+n}{k^2}}$

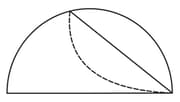
A semicircular paper is folded along a chord such that the folded circular arc is tangent to the diameter of the semicircle. The radius of the semicircle is $4$ units and the point of tangency divides the diameter in the ratio $7:1.$ If the length of the crease (the dotted line segment in the figure) is $l$ then determine $l^2.$

Let $ABC$ be an acute-angled triangle and $P$ be a point in its interior. Let $P_A, P_B$ and $P_C$ be the images of $P$ under reflection in the sides $BC, CA,$ and $AB,$ respectively. If $P$ is the orthocentre of the triangle $P_A{P}_B{P}_C$ and if the largest angle of the triangle that can be formed by the line segments $PA, PB,$ and $PC$ is $x°,$ determine the value of $x.$

Let $ABC$ be a triangle such that $AB=AC$. Suppose the tangent to the circumcircle of $ABC$ at $B$ is perpendicular to $AC$. Find $\angle ABC$ measured in degrees.

The centre of the circle passing through the midpoints of the sides of an isosceles triangle $ABC$ lies on the circumcircle of triangle $ABC$. If the larger angle of triangle $ABC$ is $\alpha °$ and the smaller one is $\beta °$, then what is the value of $\alpha -\beta$?

A friction-less board has the shape of an equilateral triangle of side length $1$ meter with bouncing walls along the sides. A tiny super bouncy ball is fired from vertex $A$ towards the side $BC.$ The ball bounces off the walls of the board nine times before it hits a vertex for the first time. The bounces are such that the angle of incidence equals the angle of reflection. The distance travelled by the ball in meters is of the form $\sqrt{N},$ where $N$ is an integer. What is the value of $N?$

Let $ABC$ be an acute angled triangle with $AB=15$ and $BC=8.$ Let $D$ be a point on $AB$ such that $BD=BC.$ Consider points $E$ on $AC$ such that $\angle DEB=\angle BEC.$ If $\alpha$ denotes the product of all possible values of $AE\mathit{,}$ find $\frac{\left[\alpha \right]}{10}$, where$\left[\alpha \right]$ is the integer part of $\alpha .$