Embibe Experts Solutions for Chapter: Sound Waves, Exercise 1: AP EAPCET - 20 Aug 2021 Forenoon

A cylindrical tube open at both ends has a fundamental frequency $f$ in air. The tube is dipped vertically in water so that $60 \%$ of the tube is in water. Then the fundamental frequency of air column is

If the length of a stretched string is shortened by $x\%$ and the tension is increased by $44\%$ then the ratio of the initial and final fundamental frequencies is $1:2$, the value of $\text{'}x\text{'}$ is

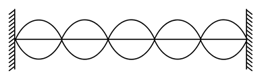
A string fixed at both ends vibrates in $5$ loops as shown in the figure. The total number of nodes and antinodes respectively are

A source is stationary and the observer is in motion along a line joining the source and the observer. If the frequency heard by the observer is $1\%$ higher than the true frequency, the ratio of velocity of the observer and that of sound in air is:

A train approaching a railway crossing at a speed of $120 \mathrm{kmph}$ sounds a whistle of frequency $576 \mathrm{Hz}$, when it is $288 \mathrm{m}$ away from the crossing. The frequency heard by the observer standing on the road perpendicular to the track from the crossing at a distance of $384 \mathrm{m}$ is (Speed of sound in air $=340 \mathrm{m} {\mathrm{s}}^{-1}$)

A small source of sound vibrating at a frequency $500 Hz$ is rotated along a circle of radius $\frac{100}{\pi }\mathrm{cm}$ at a constant angular speed of $5$ revolutions per second. The minimum and maximum frequency of the sound observed by a listener situated in the plane of the circle is (Speed of sound is $332 {\mathrm{ms}}^{-1}$)

The sources of sound $A$ and $B$ produce a wave of $350 \mathrm{Hz}$ in same phase. A particle $P$ is vibrating under an influence of these two waves. If the amplitudes at $P$ produced by the two waves is $0.3 \mathrm{mm}$ and $0.4 \mathrm{mm}$, the resultant amplitude of the point $P$ will be, when $AP-BP=25 \mathrm{cm}$ and the velocity of sound is $350 \mathrm{m} {\mathrm{s}}^{-1}$.

In case of a forced vibration, the resonance wave becomes very sharp when the: