Embibe Experts Solutions for Exercise 1: SAT 2019
Embibe Experts Scholastic Aptitude Test (SAT) Solutions for Exercise - Embibe Experts Solutions for Exercise 1: SAT 2019
Attempt the free practice questions from Exercise 1: SAT 2019 with hints and solutions to strengthen your understanding. EMBIBE CHAPTER WISE PREVIOUS YEAR PAPERS FOR SAT solutions are prepared by Experienced Embibe Experts.
Questions from Embibe Experts Solutions for Exercise 1: SAT 2019 with Hints & Solutions
Two circles, both of radii ‘’ touch each other and each of them touches internally a circle of radius . Then the radius of the circle which touches all the three circles is
Let be the vertices of the triangle If a circle passes through the vertices of then the area (in sq. units) lying inside the circle but outside the is
Let be the centroid of the triangle in which the angle is obtuse. Let and are the medians from and on the sides and respectively. If the four points and are concyclic, then
Let be a triangle with sides . Then lengths of medians of the triangle formed by the medians of the triangle are
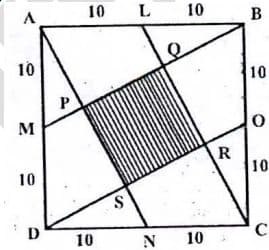
Let be a square of side . The area of the square (in ) interior to , shown in the figure is
Let be a point on the side of a triangle such that . If , then the side of an equilateral triangle whose area is equal to the area of the rectangle with sides and is
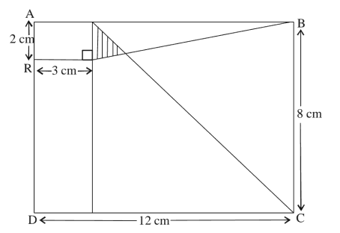
In the given figure, is a rectangle. Then the area of the shaded region is
In quadrilateral , and is a square constructed on side in the exterior of the quadrilateral . If , then the area (In ) of the square lies between.
