Embibe Experts Solutions for Chapter: Application of Derivatives, Exercise 3: Level 3

The number of the tangents that can be drawn to the curve $y^2-2x^3-4y+8=0$ from the point $(1,2)$, is

Let $f\left(x\right)$ be a polynomial of degree four having extreme values at $x=1$ and $x=2$. If $\underset{x\to 0}{\lim }\left[1+\frac{f\left(x\right)}{x^2}\right]=3$, then $f\left(2\right)$ is equal to

Rectangles are inscribed in a circle of radius $r$. The dimensions of the rectangle which has the maximum area, are

The minimum value of $\frac{\tan \left(x+\frac{\pi }{6}\right)}{\tan x}$ is

A point on the hypotenuse of a triangle is at distances $a$ and $b$ from the sides of the triangle, then the minimum length of the hypotenuse is

If the vertices of a triangle are $\left(0,0\right), \left(x,\cos x\right)$ and $\left({\sin }^{3}x,0\right)$, where $0<x<\frac{\pi }{2}$. Then, the maximum area for such a triangle (in sq.units), is

The minimum value of $\alpha$ for which the equation $\frac{4}{\sin x}+\frac{1}{1-\sin x}=\alpha$ has at least one solution in $\left(0,\frac{\pi }{2}\right)$ is______.

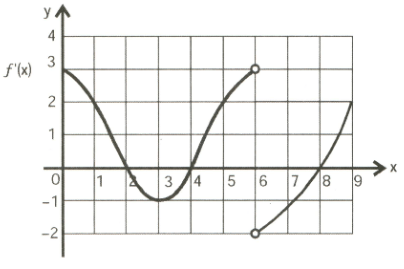
The graph of the derivative $f^{\text{'}}$ of a continuous function $f$ is shown with $f\left(0\right)=0.$ If

(i) $f$ is monotonic increasing in the interval $\left[a, b\right)\cup \left(c, d\right)\cup \left(e, f\right]$ and decreasing in $\left(p, q\right)\cup \left(r, s\right)$.

(ii) $f$ has local minima at $x=x_1$and $x=x_2$.

(iii) $f$ is concave up in $\left(\mathcal{l}, m\right)\cup \left(n, t\right]$.

(iv) $f$ has inflection point at $x=k$.

(v) number of critical points of $y=f\left(x\right)$ is $\text{'}w\text{'}$.

The value of $\left(a+b+c+d+e\right)+\left(p+q+r+s\right)+\left(\mathcal{l}+m+n\right)+\left(x_1+x_2\right)+\left(k+w\right)$ is