Embibe Experts Solutions for Chapter: Circle, Exercise 3: Level 3

If $a>2b>0$, then the positive value of $m$, for which $y=mx-b\sqrt{1+m^2}$ is a common tangent to $x^2+y^2=b^2$ and ${\left(x-a\right)}^2+y^2=b^2$ is

The diameter $AB$ of a circle of radius $2$ is extended to a point $D$ outside the circle so that $BD=3.$ Point $E$ is chosen so that $ED=5$ and the line $ED$ is perpendicular to the line $AD$. Segment $AF$ intersects the circle at point $C$ between $A$ and $E.$ The area of $∆ABC$ is $\frac{P}{S}$, where $P$ and $S$ are co-prime. What is $P-2S?$

Let $CD$ be a chord of a circle ${\Gamma }_1$ and $AB$ a diameter of ${\Gamma }_1$ perpendicular to $CD$ at $N$ with $AN>NB.$ A circle ${\Gamma }_2$ centred at $C$ with radius  $CN$ intersects ${\Gamma }_1$ at points $P$ and $Q,$ and the segments $PQ$ and $CD$ intersect at $M.$ Given that the radii of ${\Gamma }_1$ and ${\Gamma }_2$ are $61$ units and $60$ units respectively, find the length of $AM.$

If circular arcs $AC$ and $BC$ have centres at $B$ and $A$, respectively, then there exists a circle tangent to both $\widehat{\mathit{A}\mathit{C}}$ and $\widehat{\mathit{B}\mathit{C}}$, and to $\overline{\mathit{A}\mathit{B}}$. If the length of $\widehat{\mathit{B}\mathit{C}}$ is $12$, then the circumference of the circle is

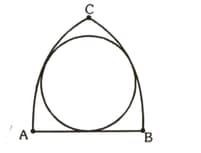
A line meets the co-ordinate axes in $A$ and $B.$ A circle is circumscribed about the triangle $OAB$. If $d_1$ and $d_2$ are the distances of the tangent to the circle at the origin $O$ from the points $A$ and $B$, respectively, then the diameter of the circle is

Let the tangent to the circle $x^2+y^2=25$ at the point $R(3,4)$ meet $x$ -axis and $y$-axis at point $P$ and $Q$, respectively. If $r$ is the radius of the circle passing through the origin $O$ and having centre at the incentre of the triangle $OPQ,$ then $r^2$ is equal to

The locus of the point of intersection of tangents to the circle $x^2+y^2=a^2,$ which are inclined at an angle $\alpha$ with each other, is

If the circle $x^2+y^2+2gx+2fy+c=0$ is touched by the line $y=x$ at point $P$ such that $OP=6\sqrt{2}$ units, where $O$ is the origin, then the value of $c$ is