Embibe Experts Solutions for Chapter: Point and Straight Line, Exercise 3: Level 3
Embibe Experts Mathematics Solutions for Exercise - Embibe Experts Solutions for Chapter: Point and Straight Line, Exercise 3: Level 3
Attempt the practice questions on Chapter 22: Point and Straight Line, Exercise 3: Level 3 with hints and solutions to strengthen your understanding. Mathematics Crash Course JEE Main solutions are prepared by Experienced Embibe Experts.
Questions from Embibe Experts Solutions for Chapter: Point and Straight Line, Exercise 3: Level 3 with Hints & Solutions
The line meets the and -axes at and , respectively. A triangle is inscribed in the triangle being the origin, with right angle at . and lie, respectively, on and . If the area of the triangle is of the area of the triangle then is equal to
Let be points on the number line such that are in be a positive proper fraction. Let be the middle point of the line segment . Then the value of is equal to
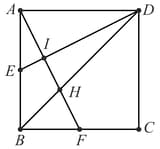
If is a square, is the midpoint of is the midpoint of and intersect at and and intersect at and the area of the quadrilateral is , find
The equation of the straight line in the normal form which is parallel to the lines and and dividing the distance between these two lines in the ratio internally is
If be any point on a line, then the range of the values of for which the point lies between the parallel lines and is
and are the inclination of lines and with -axis. If and pass through , then equation of one of the angle bisector of these lines is
If the orthocenter of the triangle formed by the lines and lies at origin, then
Let be the centroid of the triangle with vertices and Let be the point of intersection of the lines and Then the line passing through the points and also passes through the point
