Embibe Experts Solutions for Chapter: Sequences and Series, Exercise 3: Level 3

Let $a, b, c, d$ and $e$ be real numbers such that $a>b>0$. If $\frac{1}{a}, \frac{1}{b}, \frac{1}{c}$ are in $\mathrm{AP}$, $b, c, d$ are in $GP$ and $c$, $d, e$ are in $AP$, then $\frac{a{b}^2}{(2a-b{)}^2}$ is equal to

In the adjoining figure, $AB=200$ units is a diameter of the circle. Points $A \text{and} B$ are given the numbers $1,1.$  The two semicircles are bisected at $C, D.$ Numbers $2, 2$ are given to $C, D.$ $($see figure$).$ Each, of the quarter circles is bisected and given the number $3$ $($see figure$).$

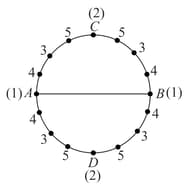
Now, each arc is bisected and the point is given the number which is the sum the two numbers at the end points of the respective arc $($see figure$).$ This process is continued till the sum of all numbers on the circle is atleast numerically equal to the product of four times the area of the circle and one third the radius. Find the least number of points plotted on the circle. $($Take $\pi =3.14).$

The coefficient of $x^{101}$ in the expansion of $(1-x)(1-2x)\left(1-2^{2}x\right)\dots \left(1-2^{101}x\right)$ is -

Statement I If $x>1,$ then sum to infinite number of $1+3\left(1-\frac{1}{x}\right)+5{\left(1-\frac{1}{x}\right)}^2+7{\left(1-\frac{1}{x}\right)}^3+\dots$ is $2x^2-x$
Statement II If $0<y<1,$ then the sum of the series $1+3y+5y^2+7y^3+\dots$ is $\frac{1+y}{(1-y{)}^2}$

If $a, b, c$ are the sides of a triangle, then $\frac{a}{b+c-a}+\frac{b}{c+a-b}+\frac{c}{a+b-c}$

Evaluate: $\left[\frac{1}{2}+\left(\frac{1}{3}+\frac{2}{3}\right)+\left(\frac{1}{4}+\frac{2}{4}+\frac{3}{4}\right)+\dots +\left(\frac{1}{100}+\frac{2}{100}+\dots +\frac{99}{100}\right)\right]$$-2400$

A sequence has first term $2007,$ after which every term is the sum of squares of the digits of the preceding term. Thus the first $3$ terms are $2007, 53\left(2^2+0^2+0^2+7^2\right), 34\left(5^2+3^2\right).$ If the sum to $2007$ terms be $S$, then $S-105000$ is

$\frac{48}{2·3}+\frac{47}{3·4}+\frac{46}{4·5}+\dots +\frac{2}{48·49}+\frac{1}{49·50}=\frac{51}{2}+k\left(1+\frac{1}{2}+\frac{1}{3}+\dots +\frac{1}{50}\right)$, then $k$ equals to