Embibe Experts Solutions for Chapter: Oscillations, Exercise 3: Level 3

A simple pendulum attached to the ceiling of a stationary lift has a time period $T$ . The distance $y$ covered by the lift moving upwards varies with time $t$ as, $y=t^2$, where $y$ is in $\mathrm{metres}$ and $t$ in $\sec$. If $g=10 \mathrm{m} {\mathrm{s}}^{-2}$, then the time period of the pendulum will be,

If the length of a simple pendulum is comparable to the radius of the earth, then find the time period for oscillation.

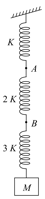
The figure alongside shows a system of springs connected to a mass $M$. The amplitude of oscillation of this system would be $\frac{mg}{3\mathrm{k}}$. What will be the ratio of the amplitudes of oscillation of points $A$ and $B$?

A particle is performing simple harmonic motion with amplitude of $4 \mathrm{cm}$ and time period of $12 \mathrm{s}$. The ratio between time taken by it in going from its mean position to $2 \mathrm{cm}$ and from $2 \mathrm{cm}$ to extreme position is
 

Two simple harmonic motions are represented by the equations $y_1=0.1\sin \left(100\mathrm{\pi }t+\frac{\mathrm{\pi }}{3}\right)$ and $y_2=0.1\mathrm{cos\pi }t$. The phase difference of velocity of the particle $1$ with respect to the velocity of particle $2$ at a time $t=0$ is

A linear harmonic oscillator of force constant $2\times {10}^6 \mathrm{N} {\mathrm{m}}^{-1}$ and amplitude $0.01 \mathrm{m}$ has a total mechanical energy of $160 \mathrm{J}$. Its

Two particles execute $\mathrm{SHM}$ of the same amplitude and frequency along the same straight line. They pass one another when going in opposite directions each time their displacement is half their amplitude. What is the phase difference between them?

The time period of a simple pendulum is given by, $T=2\pi \sqrt{\frac{l}{g}}$. In an experiment, the length of the pendulum is increased by $1\%$ while the acceleration due to gravity is also increased by $2\%$. The time period will,