Embibe Experts Solutions for Chapter: Rotational Motion, Exercise 2: Level 2
Embibe Experts Physics Solutions for Exercise - Embibe Experts Solutions for Chapter: Rotational Motion, Exercise 2: Level 2
Attempt the practice questions on Chapter 5: Rotational Motion, Exercise 2: Level 2 with hints and solutions to strengthen your understanding. Physics Crash Course JEE Main solutions are prepared by Experienced Embibe Experts.
Questions from Embibe Experts Solutions for Chapter: Rotational Motion, Exercise 2: Level 2 with Hints & Solutions
A uniform square wooden sheet of side a has its centre of mass located at point as shown in the figure on the left. A square portion of side of this sheet is cut out to produce and -shaped sheet as shown in the figure on the right.
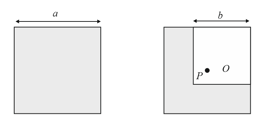
The centre of mass of the L-shaped sheet lies at the point (in the diagram) when,
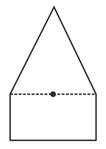
Two uniform plates of the same thickness and area but of different materials, one shaped like an isosceles triangle and the other shaped like a rectangle are joined together to form a composite body as shown in the figure. If the centre of mass of the composite body is located at the midpoint of their common side, the ratio between masses of the triangle to that of the rectangle is,
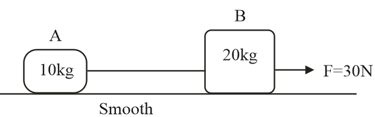
Two blocks and are connected by a massless string (shown in the figure). A force of is applied on block . The distance travelled by centre of mass in starting from rest is:
A uniform rod of mass is hinged at a point from one end of the rod and is at rest. An impulse is imparted on the other end of the rod perpendicular to it. The angular speed of the rod just after the application of the impulse is:
Four identical thin rods each of mass and length form a square frame. Moment of inertia of this frame about an axis through the centre of the square and perpendicular to its plane is . Find the value of .
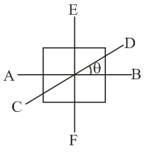
Let be the moment of inertia of a uniform square plate about an axis that passes through its centre and is parallel to two of its sides. is a line in the plane of the plate that passes through the centre of the plate and makes an angle with as shown in figure. The moment of inertia of the plate about the axis is then equal to
Moment of inertia of a circular wire of mass and radius about a tangent perpendicular to its plane:
A train is moving slowly at next to a railway platform. A man, tall, alights from the train such that his feet are fixed on the ground. Taking him to be a rigid body, the instantaneous angular velocity (in ) is
