Embibe Experts Solutions for Chapter: Gravitation, Exercise 2: Exercise#2

A body moves in a circular orbit of radius $R$ under the action of a central force. The potential due to the central force is given by, $V\left(r\right)=kr$ ($k$ is a positive constant). The period of revolution of the body is proportional to,

If the axis of rotation of the earth were extended into space, then it would pass close to,

A ball is launched from the top of Mount. Everest which is at an elevation of $9000 \mathrm{m}$. The ball moves in a circular orbit around the earth. The acceleration due to gravity near the earth's surface is $g$. The magnitude of the ball's acceleration while in orbit is,

A planet is orbiting the sun in an elliptical orbit. Let $U$ denotes the potential energy and $K$ denotes the kinetic energy of the planet at an arbitrary point in the orbit. Choose the correct statement.

The international space station is maintained in a nearly circular orbit with a minimum altitude of $330 \mathrm{km}$ and a maximum of $410 \mathrm{km}$. An astronaut is floating in the space station's cabin. The acceleration of astronaut as measured from the earth is,

An object is propelled vertically to a maximum height of $4R$ from the surface of a planet of radius $R$ and mass $M.$ The speed of the object when it returns to the surface of the planet is

Two satellites $S_1$ and $S_2$ are revolving around a planet in the opposite sense in coplanar circular concentric orbits. At time $t=0,$ the satellites are farthest apart. The periods of revolution of $S_1$ and $S_2$ are $3 \mathrm{h}$ and $24 \mathrm{h}$ respectively. The radius of the orbit of $S_1$ is $3\times {10}^4 \mathrm{km}.$ Then the orbital speed of $S_2$ as observed from

A star mass $M$ (equal to the solar mass) with a planet (much smaller than the star) revolves around the star in a circular orbit. The velocity of the star with respect to the centre of mass of star-planet system is shown below:

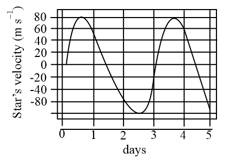
The radius of the planet's orbit is closest to ($1 \mathrm{AU}=\mathrm{Distance} \mathrm{Earth} \mathrm{and} \mathrm{Sun}$)