Embibe Experts Solutions for Chapter: Rational Numbers, Exercise 1: Exercise

Which of the following rational numbers are equivalent to $-7\frac{4}{6}$?

Sudha's teacher asked her to find the number of rational numbers between $\sqrt{2}$ and $\sqrt{3}$. Her teacher told her that $\sqrt{2}\approx 1.414$ and $\sqrt{3}\approx 1.732$. The teacher also told Sudha that $\sqrt{2}$, and $\sqrt{3}$ are not rational numbers.

How many rational numbers can be found between $\sqrt{2}$ and $\sqrt{3}$?

A ball is dropped from a height as indicated in the figure below. It goes deep into a pit, rebounds at the bottom of the pit, and goes up to $\frac{2}{3}$ of its previous height.

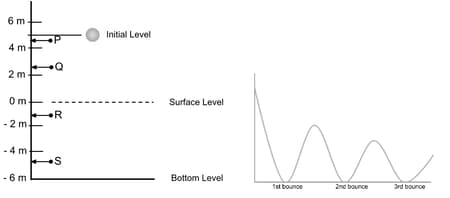
Which of these gives the ball's closest position when its reaches its maximum height between its $2$nd and $3$rd bounce? (The second figure is not to scale)

Shown below a number line drawn by Banu. She has a toy frog, which she set on $-4$ and made it to jump in the direction shown.

Each leap of the toy frog is $\frac{4}{7}$ units. In how many jumps will it be closest to $+1$ mark?

Four balances, $P, Q, R$, and $S$ are shown below. 

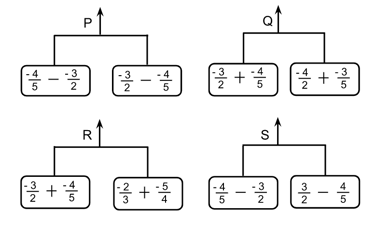
In which of the balances shown above do its respective pans hold equivalent expressions of rational numbers?

Anil drew a number line, which is given below.

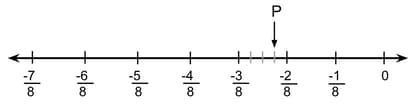
Which of the following is the number indicated by $P$ in the above number line?

The area of a circle is given by the formula, $A=\mathrm{\pi }{r}^2$, where $r$ is the radius of the circle.

Anup has two circles, $A$, and $B$ of radii $\frac{3}{7} \mathrm{m}$ and $\frac{4}{7} \mathrm{m}$ respectively. He wants to create another circle, $C$, whose area is equal to the sum of the area of the two circles, $A$, and $B$.  What should be the radius of the circle, $C$?

Dilip has a jar of paper slips with some numbers written on them. He has a machine that scans each paper slip and in the end gives the count of rational numbers. Given below are the rational numbers on the paper slips.

$\left(\frac{-3}{1.2}\right), \left(0.58\right), 2, \left(\frac{{\displaystyle 0.75}}{3.1}\right), \frac{1}{2}, 0$

What will be the count of rational numbers given by Dilip's machine?