Embibe Experts Solutions for Chapter: Triangles, Exercise 1: Exercise

In the figure below, $O$ is the centre of the circle. $A$ and $B$ are points on the circle. $\angle OAP$ and $\angle OBP$ are right angles.

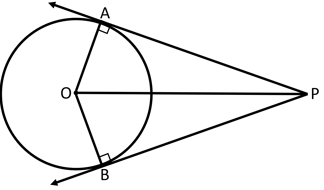
Which of the following congruence rules can we use to prove $PA=PB$?

Shown below are some triangles which Salim constructed: $△OAB, △OAC, \mathrm{and} △OAD$

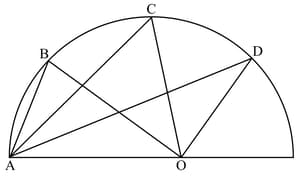
Now he wants to construct one more triangle $△OAE$, such that $OA+OE=AE$.

He marks point $E$ on the circle and joined $E$ with points $A$ and $O$.

Which of the following constructions could he have made?

In the figure below, $QM$is the median of $∆PQR$. $QM$is extended to $S$ to get $QS$. $PT\perp QM$, where $T$ is a point on $QM$ and $RS\perp QS$.

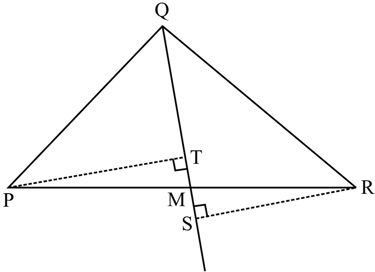
Which of these is congruence rule(s) can we apply to prove $PT=RS$?

In a triangle with integer side lengths, one side is three times as long as the second side and the length of the third side is $17$ units. What is the greatest possible perimeter of the triangle.

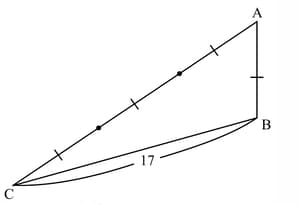
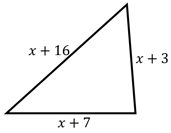
The three side lengths of a non-degenerate triangle are $x+3, x+7$ and $x+16$. Which of the following is NOT a possible value for $x?$

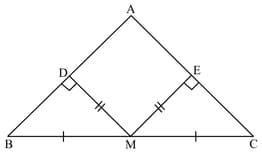
In $△ABC$ above, $\angle A=66°, M$ is the midpoint of side $\overline{BC}$, and $D$ and $E$ are the feet of perpendicular drawn from $M$ to $\overline{AB}$ and  $\overline{AC}$, respectively. If $\left|\overline{MD}\right|=\left|\overline{ME}\right|$, what is the measure of $\angle CME$?

Two brothers, Ravi and Deepak, jointly own a piece of land which is in the shape of the below figure and where $\angle B<\angle A$ and $\angle C<\angle D$.

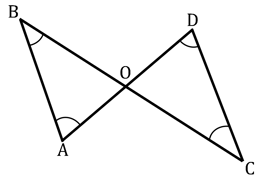
They want to put a fence along the lines $AD$ and $BC$ of the land. They come to an agreement that Ravi would put a fence along the line $AD$ and Deepak would put a fence along $BC$. Both of them argue that their length of fence is greater than the other's.

Show that, the length of the fence which Ravi has to put is less than that of Deepak.

Shivam was gifted a prism on his birthday. He found that it is a triangular prism whose base is an isosceles triangle. He drew the top view of the prism as shown below:

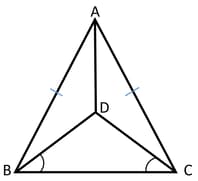
In $△ABC$, $AB=AC$. $D$ is a point in the interior of $△ABC$ such that $\angle BCD=\angle CBD$. Prove that, $AD$ bisects $\angle BAC$ of $△ABC$.