R Chandra Solutions for Chapter: Introduction to Euclid's Geometry, Exercise 1: TEST YOUR SKILLS

If $\mathrm{A},\mathrm{B}$ and $\mathrm{C}$ are three points on a line, and $\mathrm{\text{'}}\mathrm{B}\mathrm{\text{'}}$ lies between $\mathrm{\text{'}}\mathrm{A}\mathrm{\text{'}}$ and ‘ $\mathrm{C}\mathrm{\text{'}}$ (as shown in the figure), then prove that: $\mathrm{A}\mathrm{B}+\mathrm{B}\mathrm{C}=\mathrm{A}\mathrm{C}$.

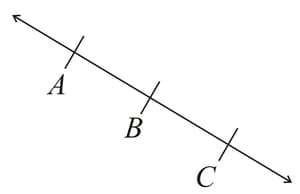
Prove that an equilateral triangle can be constructed on any given line segment.

Prove that two distinct lines cannot have more than one point in common.

Is the following statement a direct consequence of Euclid's fifth postulate?
"There exists a pair of straight lines that are everywhere equidistant from one another."

Hint: Use play fairs axiom, which is equivalent to Euclid's fifth postulate.

Attempts to prove Euclid's fifth postulate using the other postulate and axioms led to the discovery of several other geometries.