G L Mittal and TARUN MITTAL Solutions for Chapter: Centre of Mass, Exercise 1: FOR DIFFERENT COMPETITIVE EXAMINATIONS

A uniform thin cylindrical disk of mass M and radius R is attached to two identical massless springs of spring constant $\mathrm{k}$ which are fixed to the wall as shown in the figure. The springs are attached to the axle of the disk symmetrically on either side at a distance d from its centre. The axle is massless and both the springs and the axle are in horizontal plane. The un-stretched length of each spring is $\mathrm{L}$. The disk is initially at its equilibrium position with its centre of mass (CM) at a distance L from the wall. The disk rolls without slipping with velocity $V_0=V_0\hat{i}$ The coefficient of friction is $\mu$

The net external force acting on the disk when its centre of mass is at displacement x with respect to its equilibrium position is?

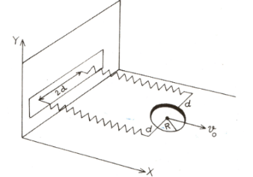
A uniform thin cylindrical disk of mass M and radius R is attached to two identical massless springs of spring constant $\mathrm{k}$ which are fixed to the wall as shown in the figure. The springs are attached to the axle of the disk symmetrically on either side at a distance d from its centre. The axle is massless and both the springs and the axle are in horizontal plane. The un-stretched length of each spring is $\mathrm{L}$. The disk is initially at its equilibrium position with its centre of mass (CM) at a distance L from the wall. The disk rolls without slipping with velocity $V_0=V_0\hat{i}$ The coefficient of friction is $\mu$

The centre of mass undergoes simple harmonic motion with angular frequency  $\mathrm{\omega }$ equal to:

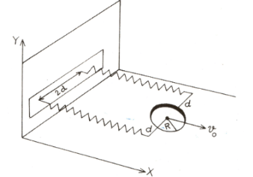
A uniform thin cylindrical disk of mass M and radius R is attached to two identical massless springs of spring constant k which are fixed to the wall as shown in the figure. The springs are attached to the axle of the disk symmetrically on either side at a distance d from its centre. The axle is massless and both the springs and the axle are in horizontal plane. The un-stretched length of each spring is L. The disk is initially at its equilibrium position with its centre of mass (CM) at a distance L from the wall. The disk rolls without slipping with velocity V0​​=V0​i^. The coefficient of friction is μ.
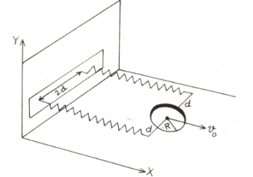
The maximum value of $V_0$ for which the disc will roll without slipping is 

Two blocks of masses $10 \mathrm{kg}, 4 \mathrm{kg}$ are connected by a spring of negligible mass and placed on a frictionless horizontal surface. An Impulse gives a velocity of $14 \mathrm{m}/\mathrm{s}$ to the heavier block in the direction of the lighter block. The velocity of the centre of mass is:

From a uniform circular disc of radius R, a coaxial smaller disc of radius $\frac{\mathrm{r}}{4}$ is moved. If  $O$ is the centre of whole disc, then the centre of mass of the remaining disc from $O$ will be will be

A system of particles contains three masses of $5 \mathrm{g}, 2\mathrm{g}$ and $3\mathrm{g}$ respectively. The respective coordinates of these particles are $\left(1, 0,-1\right), \left(1, 2,1\right),and \left(1,1,-3\right).$ The centre of mass of the system is at:

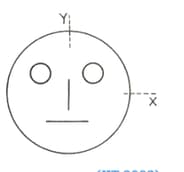
The drawing in the figure is drawn with the ink of uniform thickness. The mass of ink used to draw each of the two inner circles, and each of the two line segments is $\mathrm{m}$. The mass of the ink used to draw the outer circle is $6 \mathrm{m}$. The coordinates of the centres of the different parts are: outer circle $(0,0)$, left circle $\left(-\mathrm{a}.\mathrm{a}\right)$, right inner circle $\left(\mathrm{a},\mathrm{a}\right)$ vertical line $\left(0.0\right)$ and horizontal line $\left(0.-a\right)$. The y-coordinate of the centre of mass of the ink in this drawing is

A thin rod of length $\mathrm{L}$ is lying along x-axis with ends at $\mathrm{X}=0 \mathrm{and} \mathrm{X}=\mathrm{L}$. Its linear density (mass/ length) varies with X as $\mathrm{k}{\left(\frac{\mathrm{x}}{\mathrm{L}}\right)}^{\mathrm{n}}$ where $\mathrm{n}$ can be zero or any positive number. If the position ${\mathrm{X}}_{\mathrm{CM}}$ of the centre of mass of the rod is plotted against $\text{'}\mathrm{n}\text{'}$.