G L Mittal and TARUN MITTAL Solutions for Chapter: Force : Newton's Laws of Motion, Exercise 3: FOR DIFFERENT COMPETITIVE EXAMINATIONS

A boy sitting on the topmost berth in the compartment of a train which is just going to stop on a railway station, drops an apple at the open hand of his brother sitting vertically below his hand at a distance of about $2 \mathrm{meters}$. The apple will fall:

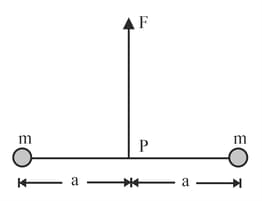
Two particles of mass $m$ each are tied at the ends of a light string of length $2a$. The whole system is kept on a frictionless horizontal surface with the string held tight so that each mass is at a distance $a$ from the centre $P$(as shown in the figure). Now the mid point of the string is pulled vertically upwards with a small but constant force $F$.  As a result, the particles move towards each other on the surface. The magnitude of acceleration, when the separation between them is $2x$ is:

Two balls, having linear momenta ${\overrightarrow{p}}_1=p\hat{i}$ and ${\overrightarrow{p}}_2=-p\hat{i}$, undergo a collision in free space. There is no external force acting on the balls. Let ${p_1}^{\text{'}}$ and ${p_2}^{\text{'}}$ be their final momenta. The following option (s) is (are) not allowed for any non-zero value of $p, a_1, a_2, b_1, b_2, c_1$ and $c_2$:

An isolated particle of mass $m$ is moving in a horizontal plane $\left(X-Y\right)$ along the $X-\mathrm{axis}$, at a certain height above the ground. It suddenly explodes into two fragments of masses $\raisebox{1ex}{$m$}\!\left/ \!\raisebox{-1ex}{$4$}\right.$ and $\raisebox{1ex}{$3m$}\!\left/ \!\raisebox{-1ex}{$4$}\right.$. An instant later, the smaller fragment is at $y=+15 \mathrm{cm}$. The larger fragment at this instant is at:

A balloon of mass $M$ is descending down with an acceleration $a\left(\mathrm{where} a<g\right)$. How much mass should be removed from it so that it starts moving up with an acceleration $a$?

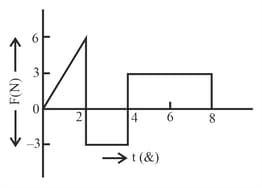
The force $F$ acting on a particle of mass $m$ is indicated by the force-time graph shown adjoining. The change in momentum of the particle over the time interval from $0 \mathrm{s} \mathrm{to} 8 \mathrm{s}$is:

A particle moves in the x-y plane under the action of a force $\overrightarrow{F}$ such that the value of its linear momentum $\overrightarrow{P}$ at any time $t$ is $p_x=2 \cos t, p_y=2\sin t$. The angle $\theta$ between $\overrightarrow{F}$ and $\overrightarrow{P}$ at a given time $t$will be:

Two particles of masses $m_1$ and $m_2$ in projectile motion have velocities $v_1$ and $v_2$ respectively at time $t=0$. They collide at time $t_o$. Their velocities become ${v_1}^{\text{'}}$ and ${v_2}^{\text{'}}$ at time $2t_o$, while still moving in the air. The value of $\left[\left(m_1{\overrightarrow{v_1}}^{\text{'}}+m_2{{\overrightarrow{v}}_2}^{\text{'}}\right)-\left(m_1{\overrightarrow{v}}_1+m_2{\overrightarrow{v}}_2\right)\right]$ is: