G L Mittal and TARUN MITTAL Solutions for Chapter: Motion in Fluids : Viscosity, Exercise 3: FOR DIFFERENT COMPETITIVE EXAMINATIONS

A small lead ball is falling freely in a viscous liquid. The velocity of the ball:

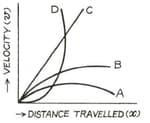
A small spherical solid ball is dropped in a viscous liquid. Its journey in the liquid is best described in the figure by:

If the terminal speed of a sphere of gold ( density$=19.5 kg{m}^{-3}$) is $0.2 m{s}^{-1}$ in a viscous liquid (density$=10.5 kg{m}^{-3}$). Find the terminal speed of a sphere of silver (density$=10.5 kg{m}^{-3}$) of the same size in the same liquid:

Spherical balls of radius $r$ Are falling in a viscous fluid of viscosity $\eta$ with a velocity $v$. The retarding viscous force acting on the spherical ball is:

The terminal velocity $v$ of a small sphere of radius $r$ falling through a viscous liquid varies with $r$ such that:

A spherical solid ball of volume $V$ is made of a material of density ${\rho }_1$. It is falling through a liquid of density ${\rho }_2 ({\rho }_2<{\rho }_1)$. Assume that the liquid applies a viscous force on the ball that is proportional to the square of its speed $v$ that is $F_{viscous}=-k{v}^2 (k>0)$. The terminal speed of the ball is:

The terminal velocity $v$ of a small steel ball of mass $m$ and radius $r$ falling under gravity through air (viscosity $\eta$) depends upon $m$, $r$, $g$ and $\eta$. Which of the following relations must be dimensionally correct?

The velocity of a small ball of mass $M$ and density $d_1$, when dropped in a container filled with glycerine becomes constant after some time. If the density of glycerine is $d_2$, the viscous force acting on the ball will be: