G L Mittal and TARUN MITTAL Solutions for Chapter: Superposition of Waves-1 : Interference and Beats, Exercise 2: NUMERICALS

Two tuning forks produce $5$ beats per second. The frequency of one is $256 \mathrm{Hz}.$ When some wax is put on the prongs of the other one, the beats disappear. Find the frequency of the second fork.

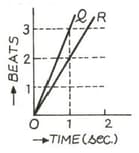
Two tuning forks A and B are sounded together. The beats produced are shown by the straight line OQ in the graph. After putting wax on the tuning fork B, they are sounded together again. The beats produced are shown by the straight line OR. If the frequency of the tuning fork A is $341 \mathrm{hertz}$, Calculate the frequency of the tuning fork B.

The frequency of a tuning fork is $256 \mathrm{Hz}$. When it is sounded with another tuning fork, $3$ beats per second are heard. When the second tuning fork is loaded with a small quantity of wax and sounded again with the first tuning fork, again $3$ beats per second are heard. What is the frequency of the second tuning fork?

The frequency of a tuning fork A is $256 \mathrm{Hz}$ . When it is sounded with a tuning fork of unknown frequency, $4$ beats per second are produced. When the prong of A is loaded with a small quantity of wax, only $1$ beat per second is heard. If the prong of A is further loaded with wax, the number of beats per second is still $1$. Determine the frequency of B. What is the final frequency of A?

Two sitar strings A and B playing the note 'Dha' are slightly out of tune and produce beats of frequency $5 \mathrm{Hz}$. The tension of the string B is slightly increased and the beat frequency is found to reduce to $3 \mathrm{Hz}$. What is the original frequency of B, if the frequency of A is $427 \mathrm{Hz}$?

$26$ tuning forks are arranged in the order of increasing frequency and any two successive forks give $4$ beats per second when sounded together. If the frequency of the last fork is three times the frequency of the first fork, then calculate the frequency of the first fork.

The wavelengths of two waves are $49$ and $50 \mathrm{cm}$. If the room temperature be $30°C,$ then how many beats per second will be heard due to these two waves? Velocity of sound at $0°C = 332 {\mathrm{ms}}^{-1}$

When, at $15°C$, an air-column and a tuning fork are sounded together, $4$ beats per second are produced. The frequency of the fork is less than that of the air-column. When the temperature falls to $10°C$, then the number of beats per second decreases by $1$. Determine the frequency of the fork. (Temperature-coefficient of sound, $\alpha =0.0036 per °C$).