G Tewani Solutions for Chapter: Area, Exercise 2: DPP

Area bounded by the $\min .\left\{\left|x\right|,\left|y\right|\right\}=1$ and the $\max .\left\{\left|x\right|,\left|y\right|\right\}=2$ is:

The area made by the curve $f\left(x\right)=\left[x\right]+\sqrt{x-\left[x\right]}$ and $x$-axis when $0\le x\le n\left(n\in N\right)$ is equal to (where $\left[x\right]$ is the greatest integer function)

Consider the regions $A=\left\{(x, y) | x^2+y^2\le 100\right\}$ and $B=\left\{\right(x, y) | \sin (x+y)>0\}$ in the plane. Then the area of the region $A\cap B$ is:

Let $R$ be the region containing the point $\left(x,y\right)$ on the $XY$-plane, satisfying $2\le \left|x+3y\right|+\left|x-y\right|\le 4$. Then the area of this region is:

If $f\left(x\right)=\left\{\begin{array}{lll}\sqrt{\left\{x\right\}}& \mathrm{for}& x\notin Z\\ 1& \mathrm{for}& x\in Z\end{array}\right.$ and $g\left(x\right)={\left\{x\right\}}^2$ where $\left\{·\right\}$ denotes fractional part of $x$, then area bounded by $f\left(x\right)$ and $g\left(x\right)$ for $x\in \left(0, 6\right)$ is:

Let $S$ is the region of points which satisfies $y^2<16x,$ $x<4$ and $\frac{xy\left(x^2-3x+2\right)}{x^2-7x+12}>0$. Its area is

The area of the region $\left\{\left(x, y\right):x^2+y^2\le 5, \Vert x|-|y\Vert \ge 1\right.\}$ is:

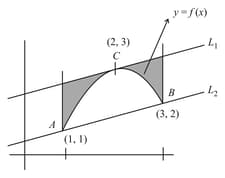
The following figure shows the graph of a continuous function $y=f\left(x\right)$ on the interval $\left[1, 3\right]$. The points $A\mathit{,}\mathit{ }B\mathit{,}\mathit{ }C$ have coordinates $\left(1, 1\right), \left(3, 2\right) \text{and} \left(2, 3\right)$, respectively, and the lines $L_1$ and $L_2$ are parallel, with $L_1$ being tangent to the curve at $C$. If the area under the graph of $y=f\left(x\right)$ from $x=1$ to $x=3$ is $4$ square units, then the area of the shaded region is: