West Bengal Board Solutions for Chapter: Geometrical Concepts Based on Different Instruments of Geometry Box., Exercise 20: Exercise 20
West Bengal Board Mathematics Solutions for Exercise - West Bengal Board Solutions for Chapter: Geometrical Concepts Based on Different Instruments of Geometry Box., Exercise 20: Exercise 20
Attempt the practice questions on Chapter 17: Geometrical Concepts Based on Different Instruments of Geometry Box., Exercise 20: Exercise 20 with hints and solutions to strengthen your understanding. GANITPRABHA (MATHEMATICS TEXT BOOK) CLASS 6 solutions are prepared by Experienced Embibe Experts.
Questions from West Bengal Board Solutions for Chapter: Geometrical Concepts Based on Different Instruments of Geometry Box., Exercise 20: Exercise 20 with Hints & Solutions
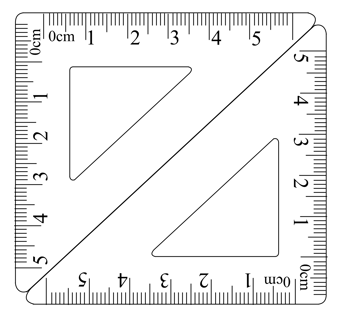
Sayan place two No. set squares together along the edges, to get a shape given below by drawing the figure with pencil on his exercise book.


It is observed that the diagram traced with pencil is a quadrilateral and is named as .
But this quadrilateral is a rectangle, since, by measuring its sides with a scale, it is found,
_____ and _____
_____
Again, it is found by measurement that _____ .
Sahana place two OIJ=set squares together along the edges, as shown in the diagram below. She traced the shape formed by set squares, in her exercise book and named it .
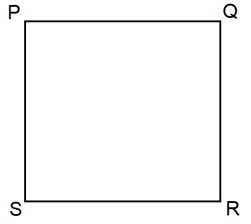
By tracing the diagram formed with two No. set squares, the figure formed is a quadrilateral. This quadrilateral is a square .
The four sides of the square were measured with scale, _____, _____, _____ and _____.
Hence, it is verified that the length of each side of a square are _____ [equal/unequal].
Again, _____.
_____ _____ _____ _____ _____.
Again, the line segments and are measured. It is found that te lengths of the line segments and are _____ [equal/unequal].
Kushal wanted to form a rectangular shape like Sayan's with two No. set squares. But by mistake he placed the set squares with different edge together, hence he got a diagram as given below. By tracing the diagram with pencil in his exercise book, he got a different figure.
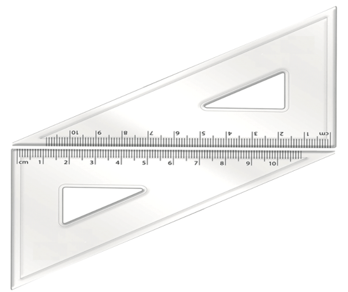
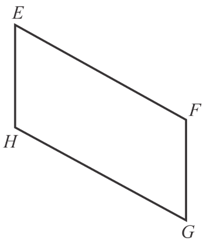
He found the figure a quadrilateral. He named it .
Now, it is found that in quadrilateral and .
That is, in quadrilateral , the opposite sides are _____ [parallel/intersecting].
By measurement, it is found that the opposite sides of the parallelogram are _____ [equal/unequal].
_____, _____, _____ & _____
Hence, the opposite angles are _____ [equal/unequal].
_____ [] (By measurement].
Again, _____ _____ _____ _____ .
We four of us, put our No. set square i.e. set square of together and traced the boundary on the paper and let us see, what we get.
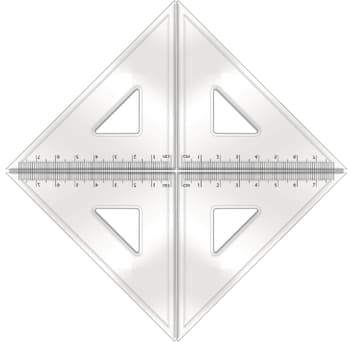
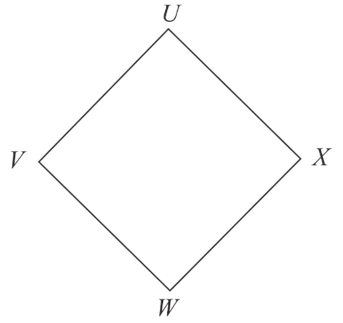
We got a quadrilateral .
By measurement, it is found that, the lengths of the sides are _____ [equal/unequal].
Measure, to get, _____ []
Measuring the angles with a protractor, we found
_____, _____, _____ & _____
In the quadrilateral , opposite angles are _____ [equal/unequal].
Again, _____.
