Goa Board Solutions for Chapter: Triangles, Exercise 3: EXERCISE
Goa Board Mathematics Solutions for Exercise - Goa Board Solutions for Chapter: Triangles, Exercise 3: EXERCISE
Attempt the practice questions on Chapter 7: Triangles, Exercise 3: EXERCISE with hints and solutions to strengthen your understanding. MATHEMATICS Textbook for Class IX solutions are prepared by Experienced Embibe Experts.
Questions from Goa Board Solutions for Chapter: Triangles, Exercise 3: EXERCISE with Hints & Solutions
and are two isosceles triangles on the same base and vertices and are on the same side of as shown in figure. If is extended to intersect at show that .
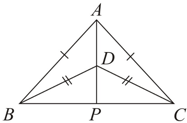
and are two isosceles triangles on the same base and vertices and are on the same side of as shown in figure. If is extended to intersect at show that bisects as well as
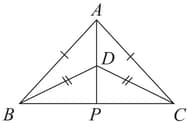
and are two isosceles triangles on the same base and vertices and are on the same side of as shown in figure. If is extended to intersect at show that is the perpendicular bisector of
is an altitude of an isosceles triangle in which Show that bisects .
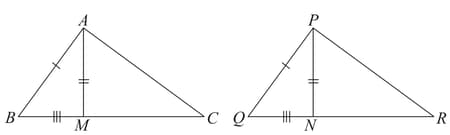
Two sides and and median of one triangle are respectively equal to sides and and median of as shown in figure. Show that .
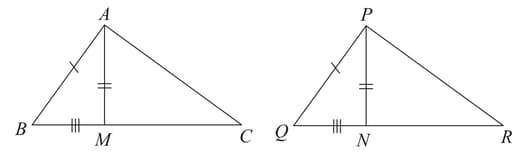
Two sides and and median of one triangle are respectively equal to sides and and median of as shown in figure. Show that
and are two equal altitudes of a triangle Using congruence rule, prove that the triangle is isosceles.
is an isosceles triangle with Draw to show that .
