H C Verma Solutions for Chapter: Rotational Mechanics, Exercise 4: EXERCISES
H C Verma Physics Solutions for Exercise - H C Verma Solutions for Chapter: Rotational Mechanics, Exercise 4: EXERCISES
Attempt the practice questions on Chapter 10: Rotational Mechanics, Exercise 4: EXERCISES with hints and solutions to strengthen your understanding. CONCEPTS OF PHYSICS [VOLUME 1] solutions are prepared by Experienced Embibe Experts.
Questions from H C Verma Solutions for Chapter: Rotational Mechanics, Exercise 4: EXERCISES with Hints & Solutions
The following figure shows a small spherical ball of mass rolling down the loop track. The ball is released on the linear portion at a vertical height from the lowest point. The circular part shown has a radius .
Find the kinetic energy of the ball when it is at a point where the radius makes an angle with the horizontal.
Find the radial and the tangential accelerations of the center when the ball is at .
Find the normal force and the frictional force acting on the ball if and .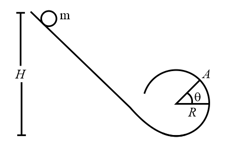
A thin spherical shell of radius lying on a rough horizontal surface is hit sharply and horizontally by a cue. Where should it be hit so that the shell does not slip on the surface?
A uniform wheel of radius is set into rotation about its axis at an angular speed This rotating wheel is now placed on a rough horizontal surface with its axis horizontal, because of friction at the contact. The wheel accelerates forward and its rotation decelerates till the wheel starts pure rolling on the surface. Find the linear speed of the wheel after it starts pure rolling.
A thin spherical shell lying on a rough horizontal surface is hit by a cue in such a way that the line of action passes through the center of the shell. As a result, the shell starts moving with a linear speed , without any initial angular velocity. Find the linear speed of the shell after it starts pure rolling on the surface.
A hollow sphere of radius lies on a smooth horizontal surface. It is pulled by a horizontal force acting tangentially from the highest point. Find the distance travelled by the sphere during the time it makes one full rotation.
A solid sphere of mass is kept on a horizontal surface. The coefficient of static friction between the surfaces in contact is . What maximum force can be applied at the highest point in the horizontal direction so that the sphere does not slip on the surface?
A solid sphere is set into motion on a rough horizontal surface with a linear speed in the forward direction and an angular speed in the anticlockwise direction as shown in figure. Find the linear speed of the sphere
when it stops rotating and
when slipping finally ceases and pure rolling starts.
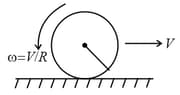
A solid sphere rolling on a rough horizontal surface with a linear speed collides elastically with a fixed, smooth, vertical wall. Find the speed of the sphere after it has started pure rolling in the backward direction?
