H C Verma Solutions for Chapter: Wave Motion and Waves on a String, Exercise 4: EXERCISES

This figure shows a wave pulse at $t=0$. The pulse moves to the right with a speed of $10 \mathrm{cm} {\mathrm{s}}^{-1}$. Sketch the shape of the string at $t=1 \mathrm{s}, 2 \mathrm{s}$ and $3 \mathrm{s}$.

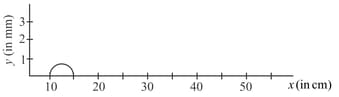
A pulse moving on a string is represented by the function, $y=\frac{a^3}{(x-vt{)}^2+a^2}$ where, $a=5 \mathrm{mm}$ and $v=20 \mathrm{cm} {\mathrm{s}}^{-1}.$ Sketch the shape of the string at $t=0, 1 \mathrm{s}$ and $2 \mathrm{s}$. Take $x=0$ in the middle of the string.

A string of length $20 \mathrm{cm}$ and linear mass density $0.40 \mathrm{g} {\mathrm{cm}}^{-1}$ is fixed at both ends and is kept under a tension of $16 \mathrm{N}$. A wave pulse is produced at $t=0$ near an end as shown in the figure, which travels towards the other end.
(a) When will the string have the shape shown in the figure again.(b) Sketch the shape of the string at a time half of that found in part (a).

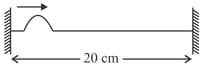
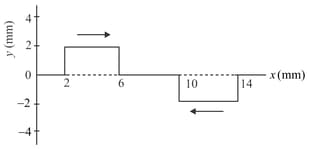
Figure shows two wave pulses at $t=0$ travelling on a string in opposite directions with the same wave speed $50 \mathrm{cm} {\mathrm{s}}^{-1}$. Point the values on graph for the string at $\mathrm{t}=4 \mathrm{ms}, 6 \mathrm{ms}, 8 \mathrm{ms},$ and $12 \mathrm{ms}$.

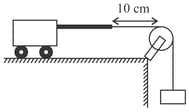
A $40 \mathrm{cm}$ wire having a mass of $3.2 \mathrm{g}$ is stretched between two fixed supports $40.05 \mathrm{cm}$ apart. In its fundamental mode, the wire vibrates at $220 \mathrm{Hz}$. If the area of cross section of the wire is $1.0 {\mathrm{mm}}^2,$ The Young modulus is given as $M\times {10}^{11} N m^{-2}$. Find the value of $M.$

The figure shows a string stretched by a block going over a pulley. The string vibrates in its tenth harmonic in unison with a particular tuning fork. When a beaker containing water is brought under the block so that the block is completely dipped into the beaker, the string vibrates in its eleventh harmonic. The density of the material of the block is given as $k\times {10}^3 kg m^{-3}$. Find the value of $k.$

A $2.00 \mathrm{m}$ long rope, having a mass of $80 \mathrm{g},$ is fixed at one end and is tied to a light string at the other end. The tension in the string is$256 \mathrm{N}$.

(a) Find the frequencies of the fundamental and the first two overtones.
(b) Find the wavelength in the fundamental and the first two overtones.

A heavy string is tied at one end to a movable support and to a light thread at the other end as shown in figure. The thread goes over a fixed pulley and supports a weight to produce a tension. The lowest frequency with which the heavy string resonates is $120 \mathrm{Hz}$. If the movable support is pushed to the right by $10 \mathrm{cm}$ so that the joint is placed on the pulley, what will be the minimum frequency at which the heavy string can resonate?