I E Irodov Solutions for Chapter: OSCILLATIONS AND WAVES, Exercise 1: MECHANICAL OSCILLATIONS
I E Irodov Physics Solutions for Exercise - I E Irodov Solutions for Chapter: OSCILLATIONS AND WAVES, Exercise 1: MECHANICAL OSCILLATIONS
Attempt the practice questions on Chapter 4: OSCILLATIONS AND WAVES, Exercise 1: MECHANICAL OSCILLATIONS with hints and solutions to strengthen your understanding. Problems in General Physics solutions are prepared by Experienced Embibe Experts.
Questions from I E Irodov Solutions for Chapter: OSCILLATIONS AND WAVES, Exercise 1: MECHANICAL OSCILLATIONS with Hints & Solutions
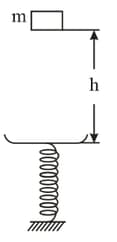
A body of mass fell from a height onto the pan of a spring balance having a mass . The mass of the spring are negligible, the stiffness of the latter is . Having stuck to the pan, the body starts performing harmonic oscillations in the vertical direction. Find the oscillation amplitude in this case.
A particle of mass moves in the plane due to the force, varying with velocity as where is a positive constant, and are the unit vectors of and axes. At the initial moment , the particle was located at the point and possessed a velocity , directed along the unit vector . Find the law of motion of the particle, and also the equation of its trajectory.
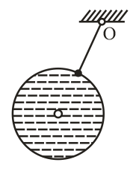
A pendulum is constructed as a light thin-walled sphere of radius , filled up with water and suspended at the point from a light rigid rod. The distance between the point and the centre of the sphere is equal to How many times will the small oscillations of such a pendulum change, after the water freezes? The viscosity of water and the change of its volume on freezing are to be neglected.
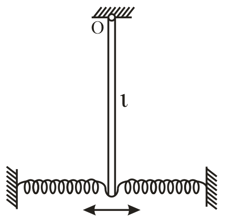
Find the frequency of small oscillations of a thin uniform vertical rod of mass and length , hinged at the point . The combined stiffness of the spring is equal to . The mass of the spring is negligible.
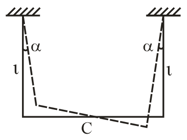
A uniform rod of mass , suspended by two identical threads, in length, was turned through a small angle about the vertical axis passing through its middle point The threads deviated in the process through an angle Then, the rod was released to start performing small oscillations. Find:
(a) the oscillation period;
(b) the rod's oscillation energy.
An arrangement illustrated in the figure, consists of a horizontal uniform disc of mass and radius , and a thin rod whose torsional coefficient is equal to Find the amplitude and the energy of the small torsional oscillations, if at the initial moment the disc was deviated through an angle from the equilibrium position and then imparted an angular velocity .
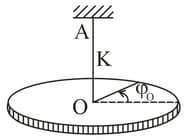
A uniform rod of mass and length performs small oscillations about the horizontal axis passing through its upper end. Find the mean kinetic energy of the rod averaged over one oscillation period, if at the initial moment it was deflected from the vertical by an angle and then, imparted an angular velocity .Assume for smaller .
A physical pendulum is positioned so that its centre of gravity is above the suspension point. From that position, the pendulum started moving toward the stable equilibrium and passed it with an angular velocity Neglecting the friction, find the period of small oscillations of the pendulum.
