HYDRODYNAMICS
I E Irodov Physics Solutions for Exercise - HYDRODYNAMICS
Simple step-by-step solutions to HYDRODYNAMICS questions of PHYSICAL FUNDAMENTALS OF MECHANICS from Problems in General Physics. Also get 3D topic explainers, cheat sheets, and unlimited doubts solving on EMBIBE.
Questions from HYDRODYNAMICS with Hints & Solutions
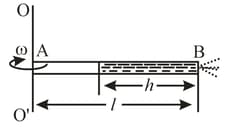
A horizontally oriented tube of length rotates with a constant angular velocity , about a stationary vertical axis passing through the end . The tube is filled with an ideal fluid. The end of the tube is open and the closed end has a very small orifice. Find the velocity of the fluid, relative to the tube, as a function of the column height .
On the opposite sides of a wide vertical vessel filled with water, two identical holes are opened, each having the cross-sectional area . The height difference between them is equal to . Find the resultant force of reaction of the water flowing out of the vessel.
The side wall of a wide vertical cylindrical vessel, of height , has a narrow vertical slit, running all the way down to the bottom of the vessel. The length of the slit is , and the width . With the slit closed, the vessel is filled with water. Find the resultant force of reaction of the water flowing out of the vessel, immediately after the slit is opened.
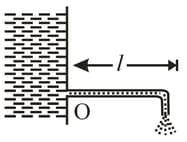
Water flows out of a big tank along a tube bent at right angles; the inside radius of the tube is equal to . The length of the horizontal section of the tube is equal to . The water flow rate is . Find the moment of reaction forces of the flowing water acting on the tube's walls, relative to the point .
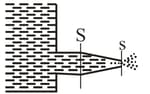
A side wall of a wide open tank is provided with a narrowing tube (as shown in the figure) through which water flows out. The cross-sectional area of the tube decreases from to The water level in the tank is higher than that in the tube. Neglecting the viscosity of the water, find the force tending to pull the tube out of the tank.
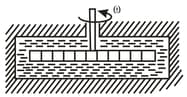
A cylindrical vessel with water is rotated about its vertical axis with a constant angular velocity . Find
(a) the shape of the free surface of the water;
(b) the water pressure distribution over the bottom of the vessel along its radius, provided the pressure at the central point is equal to .
A thin horizontal disc of radius is located within a cylindrical cavity filled with oil, whose viscosity (figure) The clearance between the disc and the horizontal planes of the cavity is equal to Find the power developed by the viscous forces acting on the disc, when it rotates with an angular velocity . The end effects are to be neglected.
A long cylinder of the radius is displaced along its axis with a constant velocity , inside a stationary co-axial cylinder of radius . The space between the cylinders is filled with viscous liquid. Find the velocity of the liquid as a function of the distance from the axis of the cylinders. The flow is laminar.
