Jitender Gupta and Divya Malik Solutions for Exercise 4: Topic Exercise

In the given figure, it shows a metal container in the form of a cylinder surmounted by a hemisphere of the same radius. The internal height of the cylinder is $7\mathrm{m}$ and the internal radius is $3.5\mathrm{m}$. Calculate the total area of the internal surface, excluding the base (in $m^2$ ).

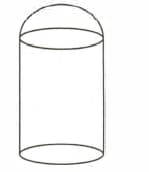
In the given figure, it shows a metal container in the form of a cylinder surmounted by a hemisphere of the same radius. The internal height of the cylinder is $7 \mathrm{m}$ and the internal radius is $3.5 \mathrm{m}$.

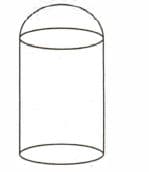
Calculate the internal volume of the container $\left(\mathrm{in} {\mathrm{m}}^3\right)$.

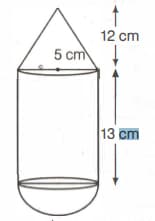
In the given figure, toy is in the shape of a right· circular cylinder with a hemisphere on one end and a cone on the other. The height and radius of the cylindrical part are $13 \mathrm{cm}$ and $5 \mathrm{cm}$,respectively. The radii of the hemispherical and conical parts are the same as that of the cylindrical part. Calculate the surface area of the toy if height of the conical part is $12 \mathrm{cm}$

The interior of a building is in the form of a cylinder of diameter $4.3 \mathrm{m}$and $3.8 \mathrm{m}$ Height, surmounted by a cone whose vertical angle is a right.angle. Find the height and slant height of the cone. Also, find the surface area of building.$\left[\mathrm{Take} \mathrm{\pi } =3.14\right]$. Write the answer in metres.

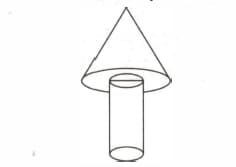
A wooden toy is in the shape of a cone mounted on a cylinder as shown in the following the figure. If the height of the cone is $24 \mathrm{cm}$ the total height of the toy is $60 \mathrm{cm}$ and the radius of the base of the cone is equal to twice the radius of the base of the cylinder is $10 \mathrm{cm}$; then find the total surface area of the toy. [Take $\mathrm{\pi }=3.14$]. (Write the decimal answer upto one decimal place with ${\mathrm{cm}}^2$.)

A container shaped like a right circular cylinder having diameter $\text{12 cm}$ and height $\text{15 cm}$is full of ice-cream. The ice-cream is to be filled into cones of height 12cm and diameter 6 cm, having a hemispherical shape on the top. Find the number of such cones which can be filled with ice- cream.

In the given figure, from a solid sphere of radius $\text{9 cm}$, a cone mounted on a hemisphere shape is carved out. The radius and height of a cone are $\text{4 cm}$and $\text{5 cm}$ Respectively. Find the surface area of the remaining figure in ${\text{cm}}^2.$

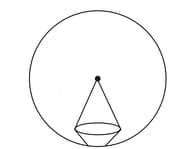
A small cone of radius $5 \mathrm{cm}$ And slant height $7 \mathrm{cm}$ Is mounted on a bigger solid cone of radius $8 \mathrm{cm}$ And slant height $12 \mathrm{cm}$ With common base. Find the surface area of the combined figure (upto one decimal  . $[$Take $\mathrm{\pi } = 3.14]$.