Jose Paul Solutions for Chapter: Chords and Angles of Circles, Exercise 1: EXERCISE 13.1
Jose Paul Mathematics Solutions for Exercise - Jose Paul Solutions for Chapter: Chords and Angles of Circles, Exercise 1: EXERCISE 13.1
Attempt the practice questions on Chapter 13: Chords and Angles of Circles, Exercise 1: EXERCISE 13.1 with hints and solutions to strengthen your understanding. Discovering Mathematics Book 8 solutions are prepared by Experienced Embibe Experts.
Questions from Jose Paul Solutions for Chapter: Chords and Angles of Circles, Exercise 1: EXERCISE 13.1 with Hints & Solutions
In the given figure, . If the radius is , then find the value of .
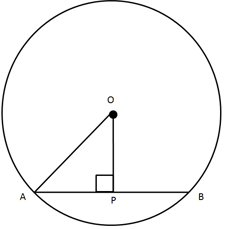
From the given data, find the length of the segment as required.
. If the distance of is then find .
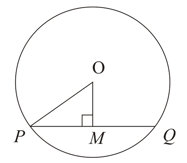
. If the radius , then find the value of .
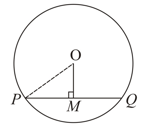
In the given figure, and if , then find .
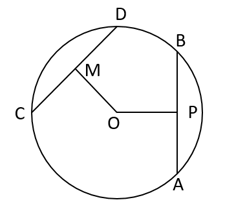
From the given data, find the length of the segment as required.
. If then find .
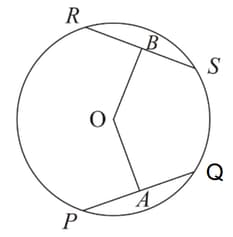
The diameter and a chord of a circle have a common endpoint as shown in the figure. If the length of the diameter is , the length of the chord is and the distance of midpoint of the chord from the centre is then find .
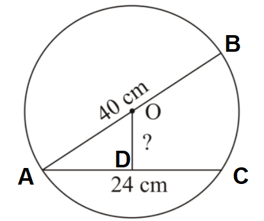
A chord whose midpoint is away from the centre of the circle is long. If the radius of the circle is , then find the value of .
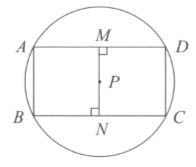
Given a circle with centre is the midpoint of . is perpendicular to as well as . Prove that is a rectangle.